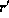The tensor notation is easy to understand.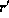 
,
the two indices are down. To have one up you use up.
A partial derivative is indicated by pup or pdn,
a covariant derivative by cup and cdn.
The Riemann tensor is R(with 4 indices), the Einstein tensor is represent as G(two indices), the Weyl tensor as C (4 indices) the Christoffel symbol as Chr ( 3indices)...
For example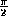 
is
notated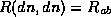 
.
The most common command are
>qload ( kerr ): >grcalc ( R(dn,dn) ):
This first loads the Kerr metric (predefined) and then calculates the component of the Ricci tensor.
>grdisplay( R(dn,dn) ):
It displays the components without any simplification.
>gralter ( R(dn,dn), trig ): >grdisplay( R(dn,dn) ):
Now trigonometric simplifications are done. There are some others simplifications possible (Maple facilities).
The coordinate changes are also done by GR-Tensor.
>grtransform (schw, kruskal, xform := [ u(r,t) = sqrt(r/(2*m)-1)*exp(r/(4*m))*cosh(t/(4*m)), v(r,t) = sqrt(r/(2*m)-1)*exp(r/(4*m))*sinh(t/(4*m)), Theta(theta) = theta, Phi(phi) = phi ] ):
This give the Schwarzschild metric in the Kruskal coordinates.