The binomial expansion tells us how to write the expression (a+b)^N in terms of a sum of various powers of a and b. The way to do this in principle is just to write out all the factors and expand term by term. For example

(a+b)² = (a+b) x (a+b) = a x (a+b) + b x (a+b)

           = aa + ab + ba + bb

           = a² + ab + ab +b²        (note: this expression has 4 terms)

           = a² + 2ab + b²

where ab = a x b, and from now on we will stop using the "x" symbol for multiplication, and just indicate multiplication by writing the two quantities next to each other.

(a+b)³ = (a+b)(a+b)(a+b) = a(a+b)(a+b) + b(a+b)(a+b)

           = aa(a+b) + ab(a+b) + ba(a+b) + bb(a+b)

           = aaa + aab + aba + abb + baa + bab + bba + bbb

           = a³ + a²b + a²b + ab² + a²b + ab² + ab² + b³      (note: the above expression has 8 terms)

           = a³ + 3a²b + 3ab² + b³

In general,

(a+b)^N = (a+b)(a+b)(a+b)...(a+b)

where "..." means there are a total of N such terms. When we expand out, each resulting term can be viewed as if it were the result of "choosing" either an "a" or a "b" from each of the N factors (a+b). Since there are two such choices for each factor (a+b), we see that we will wind up with 2^N terms (check that this agrees with the above cases: for N=2 we found 2²=4 terms, for N=3 we found 2³=8 terms).

Consider now the particular case where we have chosen "b" r times and hence "a" is chosen the remaining N-r times, we wind up with the term a^N-rb^r. There will be many such terms a^N-rb^r for a given value of r, as there are many different ways to choose the r "b"s from the N factors (a+b). How many ways are there? There are exactly ^NC_r ways! So when we expand (a+b)^N, the term a^N-rb^r appears                times. We thus can group them all together into a single term:

Now there will such terms for all values of r = 0, 1, 2, ..., N. Note that for the term r=0 we choose "b" no times, and choose "a" N times. The resulting factor, a^N, is consistent with the above formula provided we regard 0!=1, as we said earlier in our definition of the factorial, and also b⁰=1. This last result b⁰=1 is consistent with the usual mathematical conventions of power laws. Similarly, for the term r=N, the above formula is consistent with b^N.

So finally we have the binomial expansion:
 
 

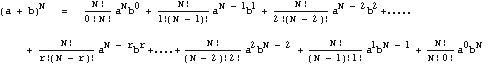
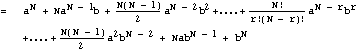
Where we use the fact that x⁰ = 1, and x¹ = x, for any number x. You can check that this formula gives the correct results for the cases N=2 and N=3 which we did explicitly above.