Problem 1 [40 points total]
Consider the classical ideal gas. In lecture, we
found that the total entropy could be written as:
S(E,V,N) = (N/No)So + NkB
ln
[ (E/Eo)3/2(V/Vo)(N/No)-5/2 ]
where E is the total internal energy, V is the total volume, and
N is the number of particles. Eo, Vo, No,
So, and kB are constants.
(a) Starting from the above S(E,V,N), find the Helmholtz free energy
A(T,V,N), the Gibbs free energy G(T,p,N), and the Grand Potential
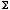(T,V,µ), by the method of Legendre transforms. [10 points]
(b) Find the familiar equation of state, pV = NkBT, by
taking an appropriate 1st derivative of an appropriate thermodynamic
potential. [5 points]
(c) Find the chemical potential µ, by taking an
appropriate first derivative of a thermodynamic potential.
Show explicitly that the chemical potential
is the same as the Gibbs free energy per particle. [5 points]
(d) Find the pressure p, by taking an appropriate first derivative
of a thermodynamic potential. Show explicitly that the pressure
is the same as the negative of the Grand Potential per volume. [5 points]
(e) By computing the appropriate 2nd derivatives of the appropriate
thermodynamic potentials, compute the specific heats CV and
Cp, the compressibilities 
T and
S, and the coefficient of thermal expansion 
. Show
that the two specific heats, and the two compressibilities, obey
the general relations found in lecture. [10 points]
(f) If one allows the gas to expand isothermally (i.e. at constant
temperature), how does the volume vary with the pressure? If one allows
the gas to expand adiabatically (i.e. at constant entropy), how does the
volume now vary with the pressure? You must show how you derive your
results. [5 points]
Problem 2 [10 points total]
Consider taking the Legendre transform of the energy, E(S,V,N), with
respect to S, V, and N, to get a new thermodynamic potential,
X(T,p,µ).
(a) Show that X(T,p,µ) is identically zero. [5 points]
(b) What does this imply about the variables T, p, and µ?
Where have you already seen this result before? [5 points]
