|
|

Home
Contact
Info
Course
Info
Calendar
Homework
Lecture
Notes
|
|
|
|
Physics 418: Statistical Mechanics I
Prof. S. Teitel stte@pas.rochester.edu ----- Spring 2006
Problem Set 2
Due Tuesday, February 28, in lecture
- Problem 1 [10 points]
A thermodynamic engine can be thought of as a cyclic
process by which heat (TdS) pumped from a "hot" reservoir into a system
(the engine) is converted into work (pdV) done by the engine.
The most famous such example is the Carnot cycle. Another
such cycle is the Otto cycle, schematically shown in the
diagram below as a directed path in the volume-entropy plane. The Otto cycle is a rough approximation
to the operation of a gasoline engine.
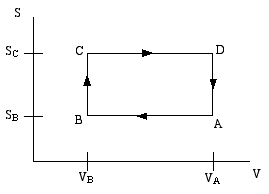
The gas is compessed adiabatically (constant entropy) in the
step A to B. Then it is heated isochorically (constant volume)
in the step B to C (this step corresponds to the combustion
of the gas in the gas engine). The gas is then expanded adiabatically
in step C to D (this is the power stroke).. Finally the gas is cooled
isochorically to bring it back to its initial state; this is step D to A.
Step B to C extracts heat QBC from the "hot" reservoir to heat the gas,
while step D to A returns heat QDA = - QAD to the "cold" reservoir (usually the
ambient atmosphere). The difference is the work done by the engine.
If the engine efficiency is defined as ratio of the net heat converted to work, divided by the heat withdran from the hot reservoir
 = (QBC - QAD)/QBC = (QBC - QAD)/QBC
then assuming the gas is an ideal gas, show that the efficiency of
the Otto cycle is given by,
 = 1 - (VB/VA)(Cp
- CV)/CV = 1 - (VB/VA)(Cp
- CV)/CV
- Problem 2 [15 points]
Consider a system of N distinguishable non-interacting
objects, each of which can be in one of two possible states,
"up" and "down", with energies +e and -e. Assume that N is large.
(a) Working in the microcanonical ensemble, find the entropy
of the system S(E, N) as a function of fixed total energy E and number N (Hint: it
is useful to consider the numbers N+ and N- of up and
down objects).
(b) Find the temperature T as a function of energy E and number N. Show
that T will be negative if E>0.
(c) What happens if such a system (1) with T1<0 comes into thermal
contact with another such system (2) with T2>0? Does T1
increase or decrease? Does T2 increase or decrease? In
which direction does the heat flow?
- Problem 3 [15 points]
Consider the same situation as in problem 1:
A system has N distinguishable non-interacting objects, each of which can be in one of two possible states, "up" and "down", with energies +e and -e. Assume that N is large. Now solve this problem using the canonical ensemble!
a) Working in the canonical ensemble, find the Helmholtz free energy A(T, N) as a function of temperature T and number N. Note: Having found 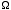 (E) in problem 2, you could compute the canoncial QN by taking the Laplace transform of (E) in problem 2, you could compute the canoncial QN by taking the Laplace transform of 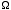 (E). Don't do it this way! Instead, compute QN by directly suming the Boltzmann factor over all states in the phase space. The point of this problem is to see that it is easier to find QN this way, than it was to find (E). Don't do it this way! Instead, compute QN by directly suming the Boltzmann factor over all states in the phase space. The point of this problem is to see that it is easier to find QN this way, than it was to find 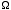 (E). Having found QN, you can then check your answer by taking the the Laplace transform of (E). Having found QN, you can then check your answer by taking the the Laplace transform of 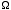 (E). (E).
b) By making the appropriate transformations on A(T, N), find the canonical entropy as a function of the average total energy E and number N. Show that your result, as N goes to infinity, agrees with the entropy you found in Problem Set 2 using the microcanonical ensemble.
- Problem 4 [10 points]
In lecture we derived the canonical partition function
QN(V,N) for the idea gas using a factorization method.
One can also directly compute it by taking the Laplace transform
of the microcanonical partition function 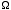 (E,V,N).
Using our result from lecture, (E,V,N).
Using our result from lecture,
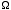 (E,V,N) = [ (E,V,N) = [ |
V
h3 |
(2 mE)3/2 mE)3/2 |
]N |
1
[(3N/2) - 1]! N! |
( /E) /E) |
compute directly the Laplace transform,
| QN(T,V) = |

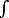
0 |
dE
 |
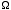 (E,V,N)e- (E,V,N)e-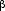 E E |
and show that you get the same result as found in lecture.
|

