January 07 2003
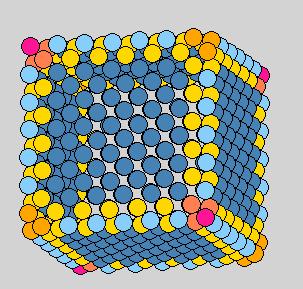
Test fitting methods with an fcc cube
An fcc cube with 1372 gold atoms have been created and gone through
the mthods. There are 508 surface atoms.
The cutoff has been selected as 4.1 Angstrom so that the numbers
of neighboring atoms range arom 6 to 8. In the icosahedral
gold cluster with cutoff of 3.8 neighboring atom numbers range from 5 to
7.
From the following results we can reach the conclusion that method 2 is the
most robust method to do fitting. That is, finding normal vector by
fixing tangent plane on center of mass of local strucuture, and do
the parabolic fitting by fixing the parabolic surface on center particle.
Normal vectors
Center-particle method failed at corners of the cube. Although both methods
should not behave much different in general cases, center-of-mass method are
more robust in extreme situations.
Center-of-mass
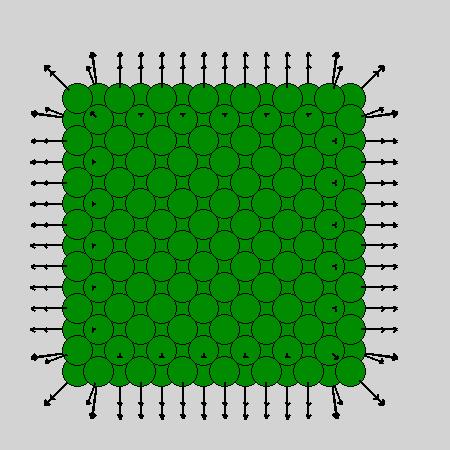
Center-particle

Histogram of flatness and bond curvature
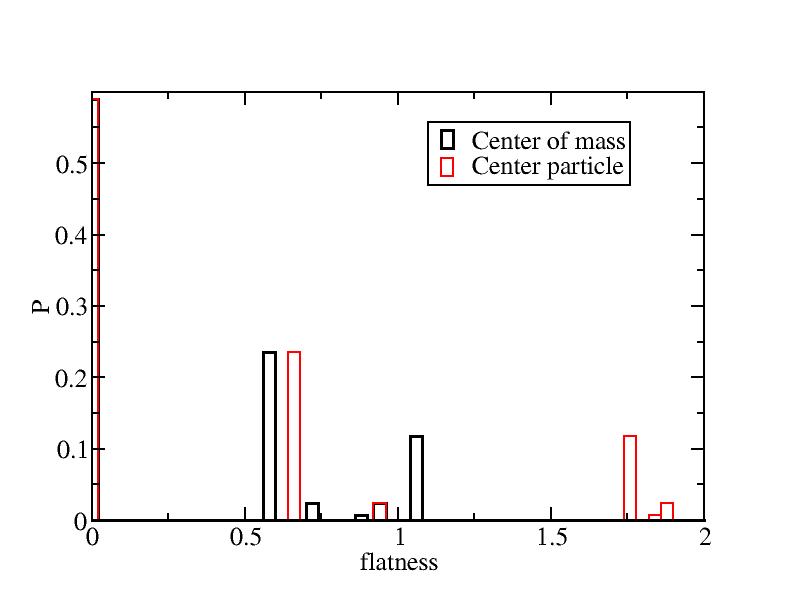
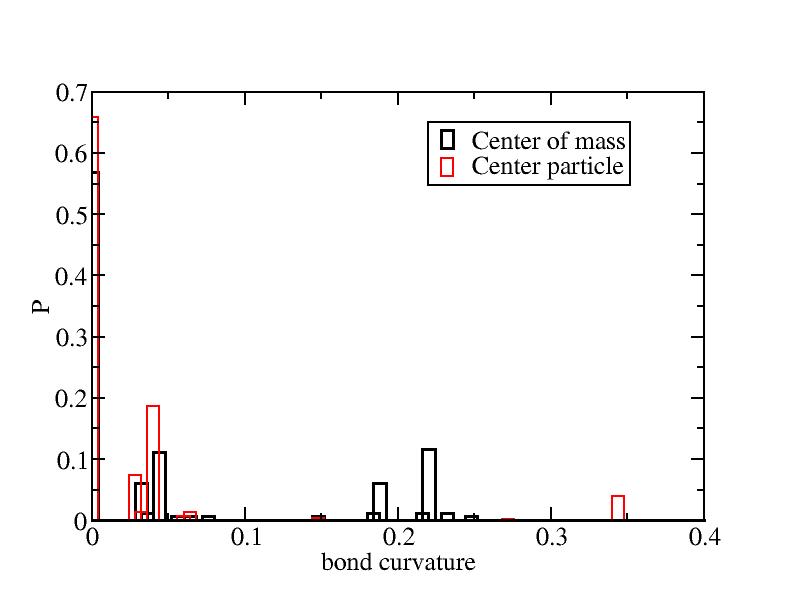
Distribution of parabolic curvatures
Because there are too few corner atoms (4 for cubes), the peak in 3D histgram
is hard to see. So 2D distribution plots with peak values have been drawn
as the following pictures.
Colored configurations according to the local curvatures
The coloring is according to the discrete region of the scatter plots of the
distributions of parabolic curvatures. They are not scaled linearly in this
case.
The coloring is principally with smaller curvature. Whenever there is a
degeneracy, larger curvature is used to distinguish.
Spectrum of coloring

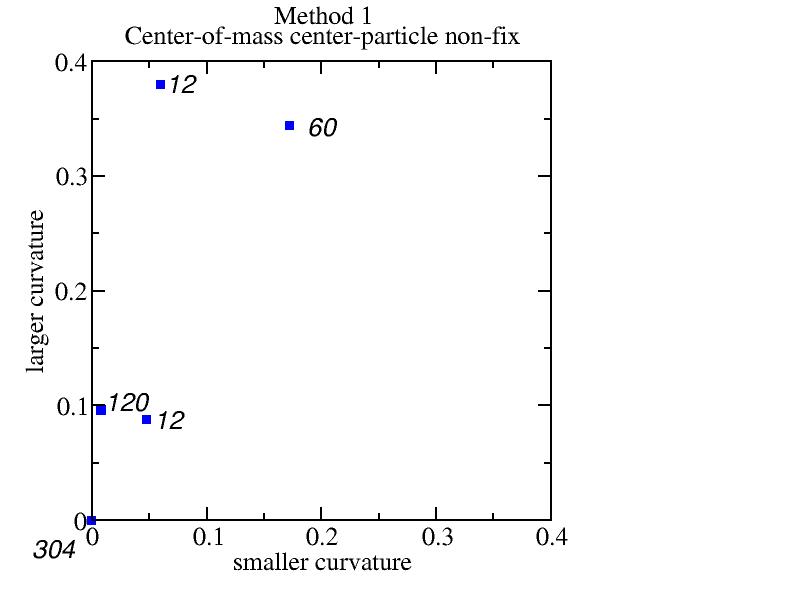
Method 1: center-of-mass center-particle non-fix
Bad because the four corner particles have (0,0) parabolic curvatures.
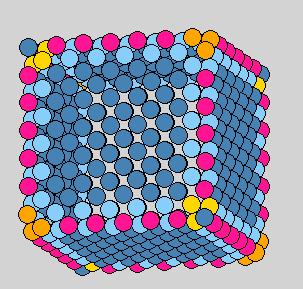
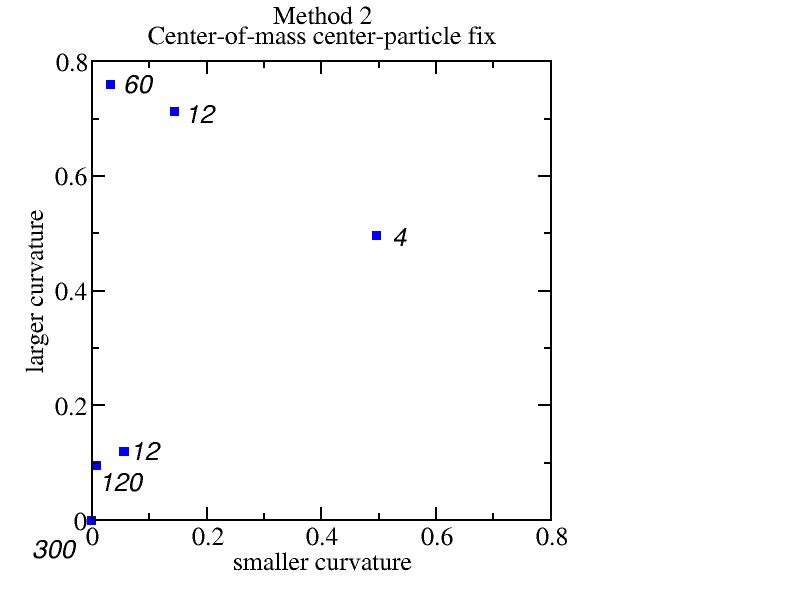
Method 2: center-of-mass center-particle fix
Good distinguishing.
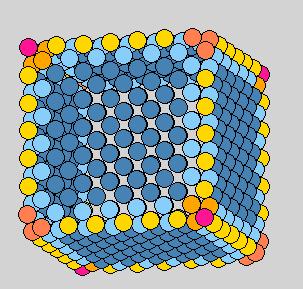
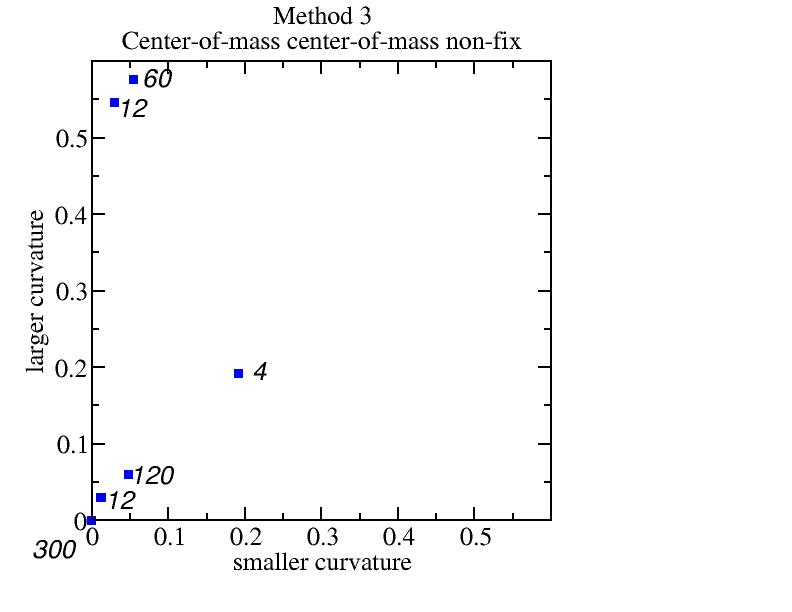
Method 3: center-of-mass center-of-mass non-fix
Bad because the 12 near-corner particles other than the four corners have
smaller curvatures than the edges.
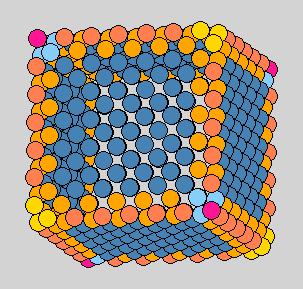
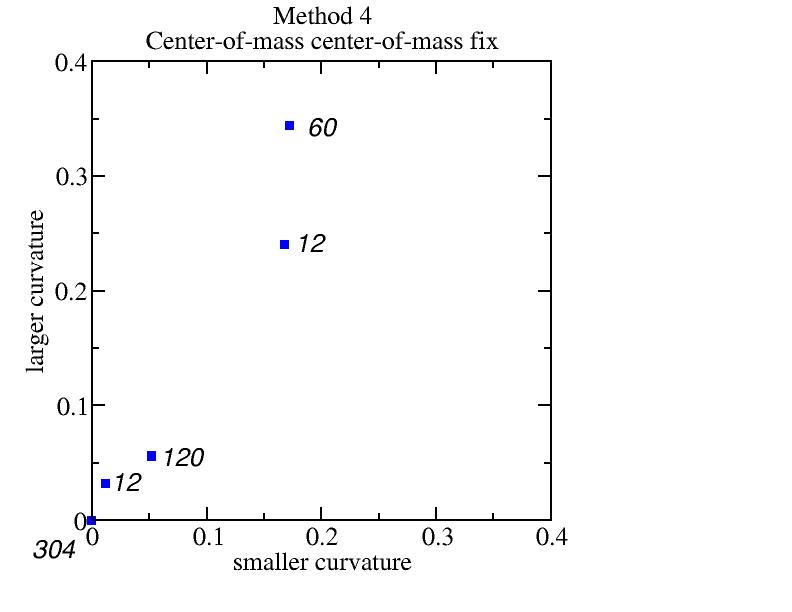
Method 4: center-of-mass center-of-mass fix
Bad because the four corner particles have (0,0) parabolic curvatures.
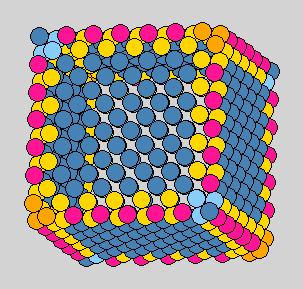
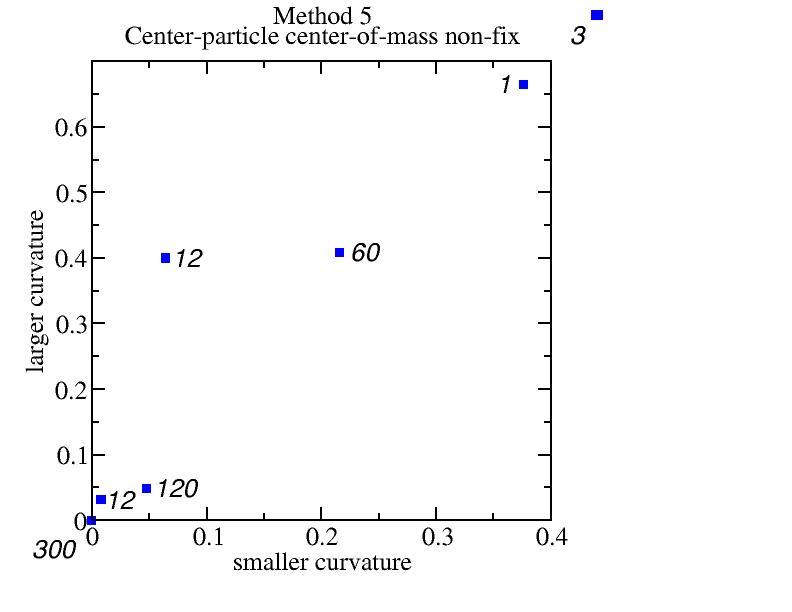
Method 5: center-particle center-of-mass non-fix
Bad because the 12 near-corner particles other than the four corners have
smaller curvatures than the edges.
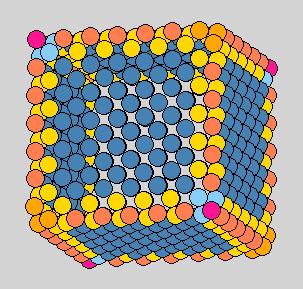
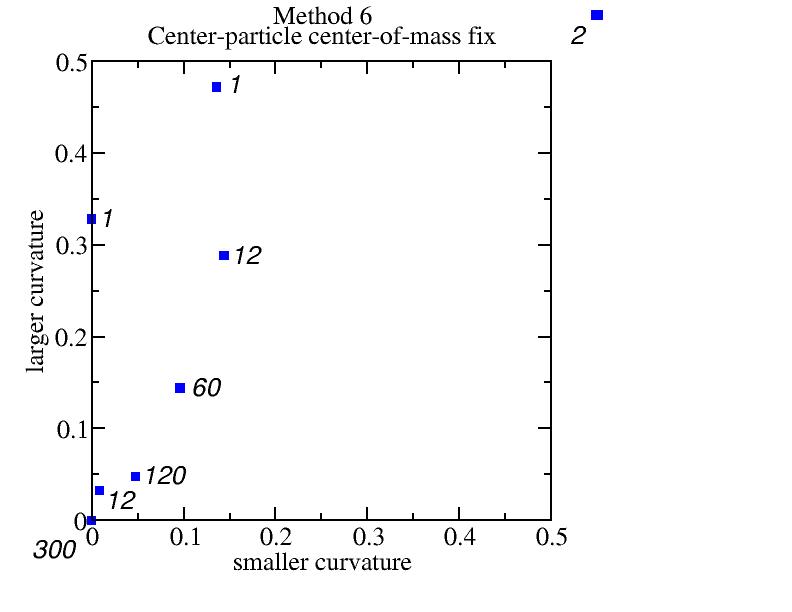
Method 6: center-particle center-of-mass fix
Bad because the four corner particles treated different and 12 near-corner
particles have smaller curvatures.
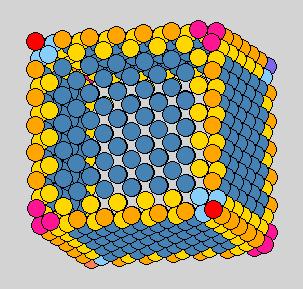
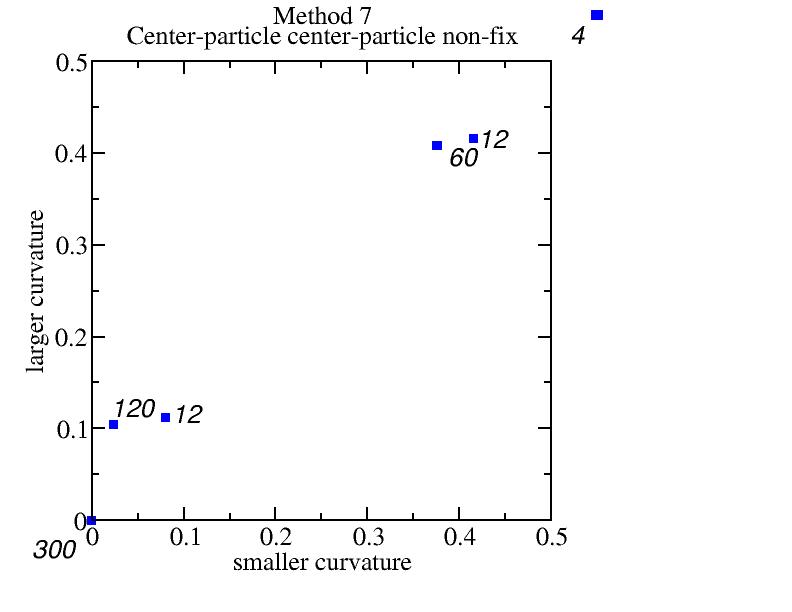
Method 7: center-particle center-particle non-fix
Not bad but because the flase normal vectors for the 4 corner particles their
curvatures are too large.
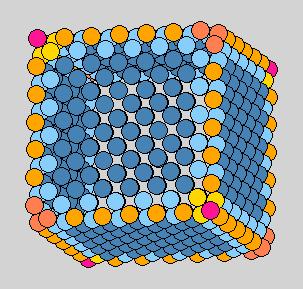
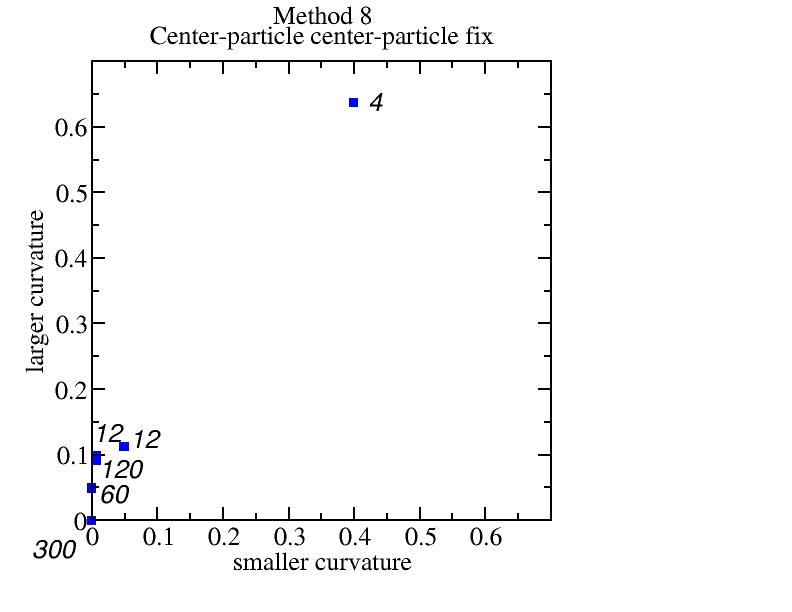
Method 8: center-particle center-particle fix
Same reason as 7 and also bad for that the edge particles have smaller
curvatures than the near-edge smaller curvatures.