June 06 2003

Shape distribution and Average shape by solid angle

Idea

At high temperatures, the atoms move around or diffuse and the macroscopic shape of the gold cluster fluctuates a lot. Even in liquid the cluster forms some faces on the surface. Despite the macroscopic fluctuations and the individual movements of the atoms, we may assume there is an equilibrium shape at each temperature level and the instantaneous shapes just fluctuate around it and form a Gaussian like distribution.

Method

To verify if the above idea is true, we put all of the surface atoms of the 1000 configurations (saved along 10^7 simulation steps (43ns) ) of each temperature level together and projected them to the x-z plane (y axis happend to be one of the principle axis of this icosahedral cluster). Those 2D plots verified that there are equilibrium shapes and distributions around them.

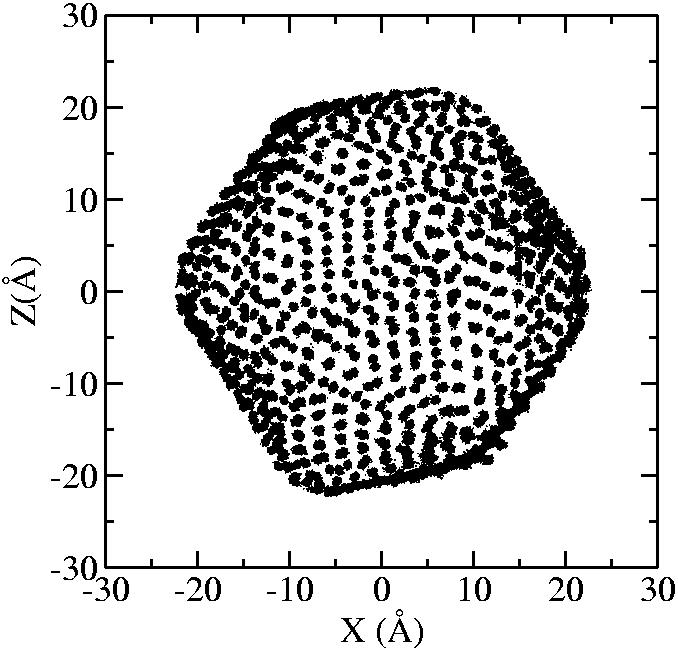
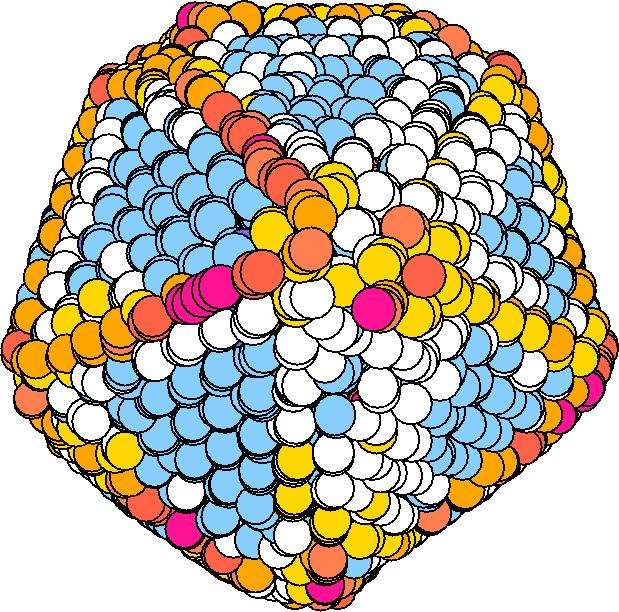
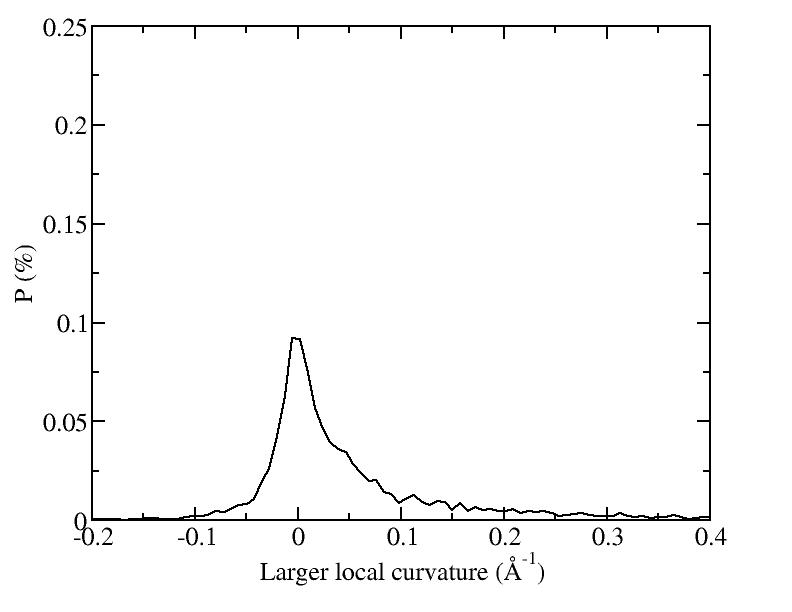
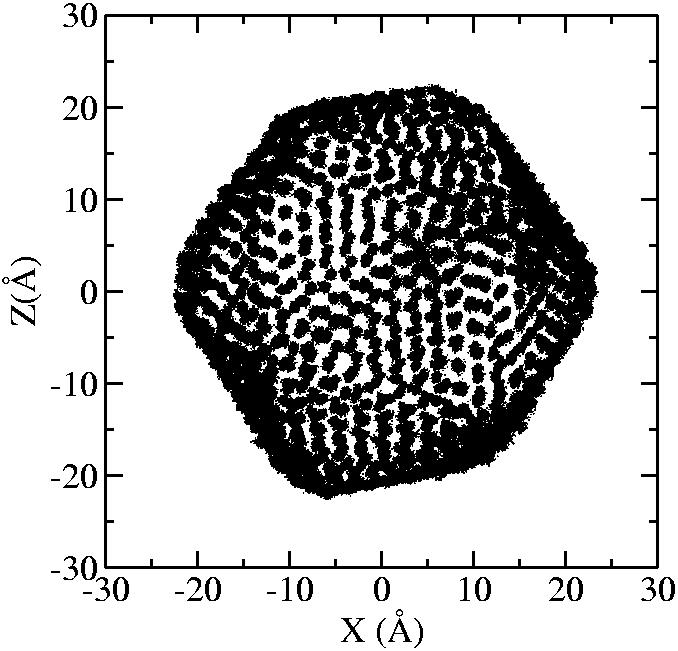
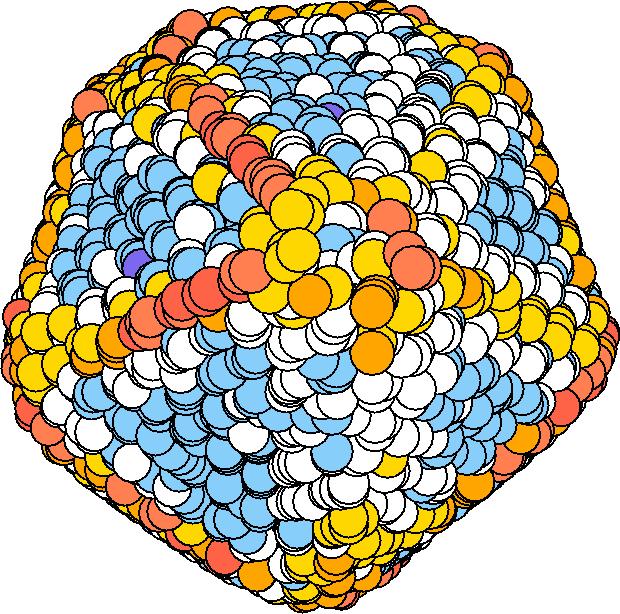
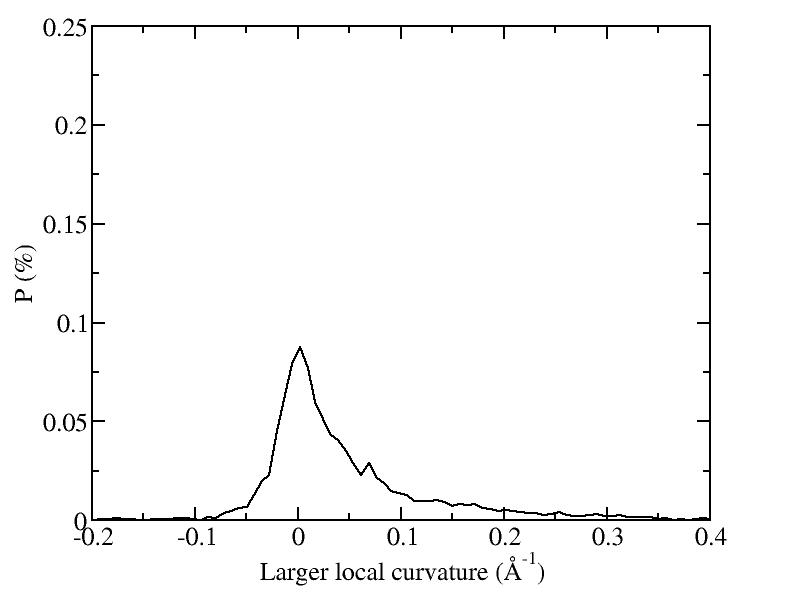
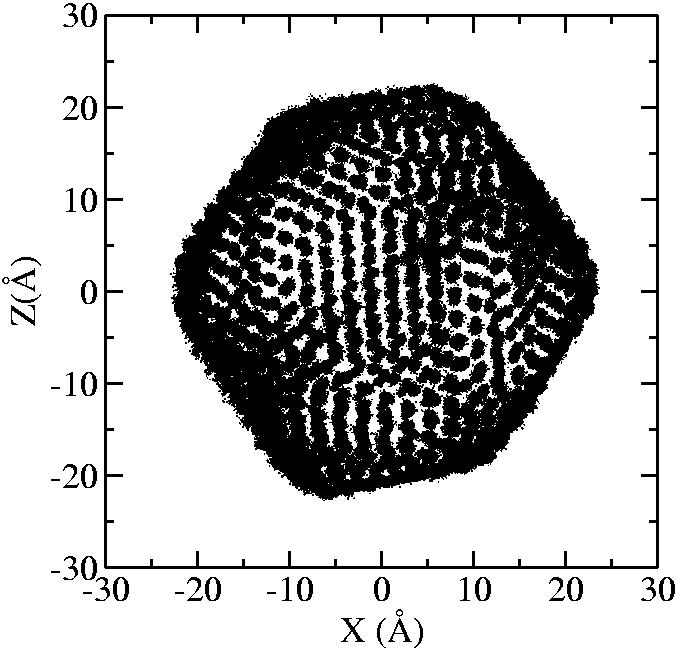
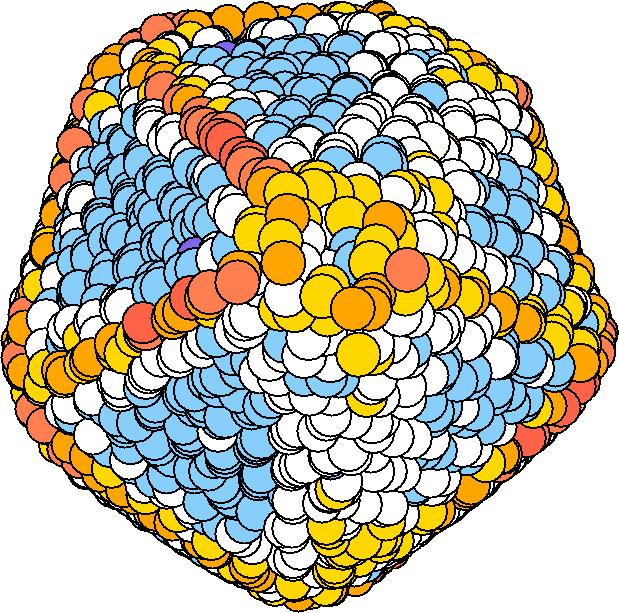
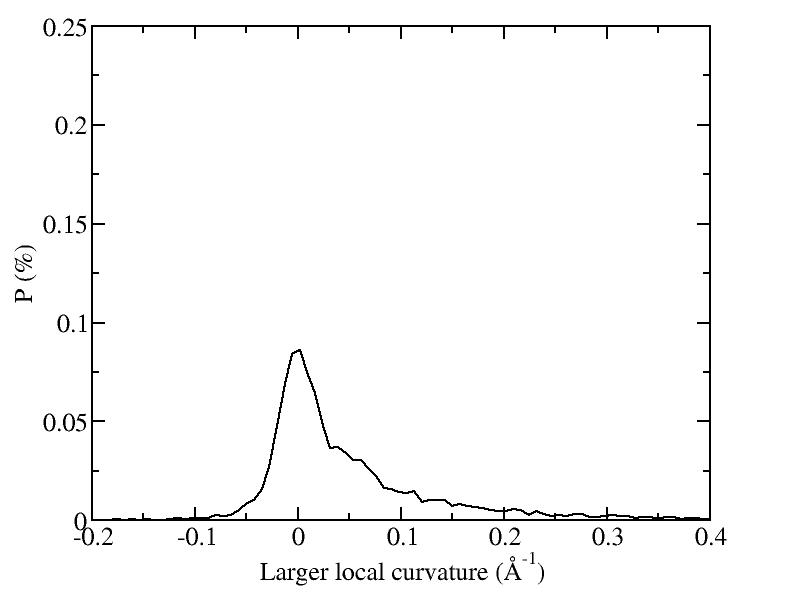
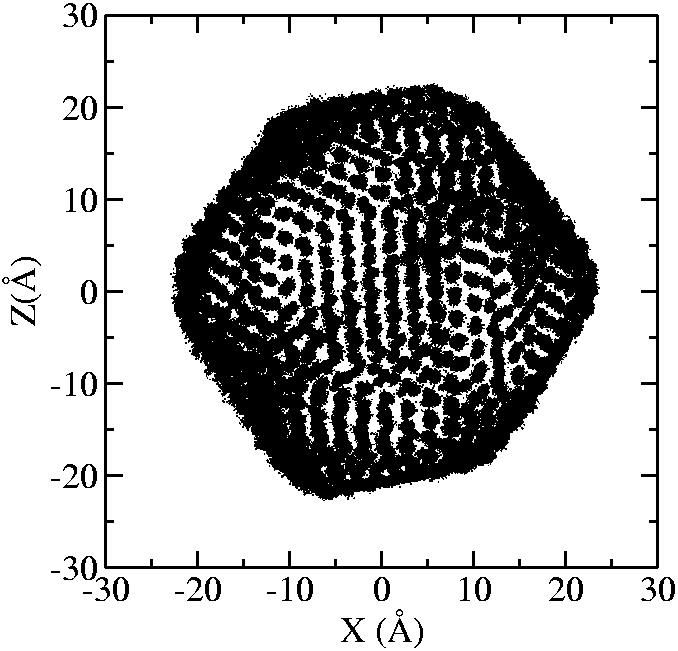
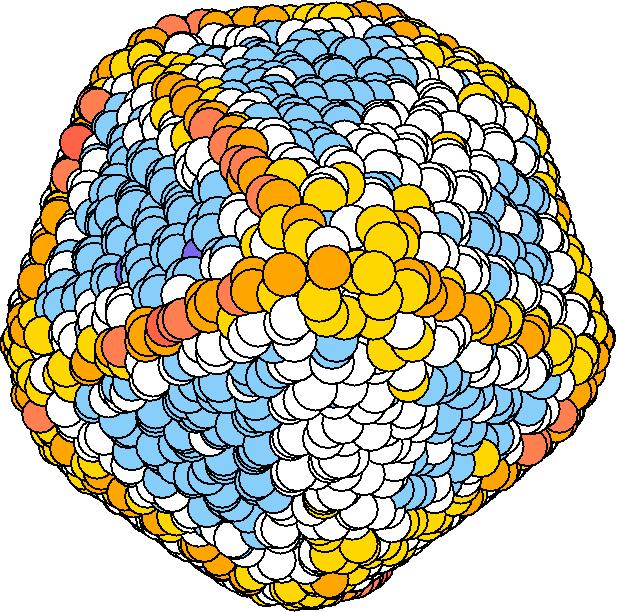
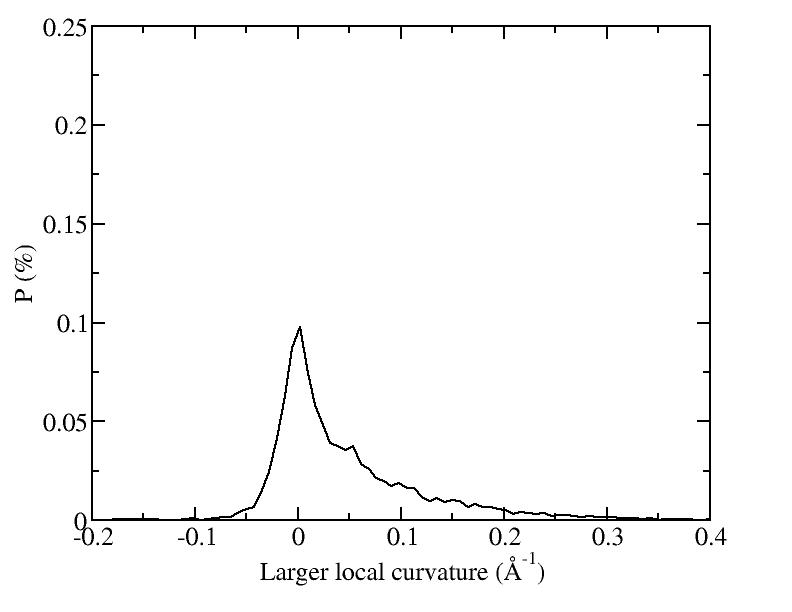
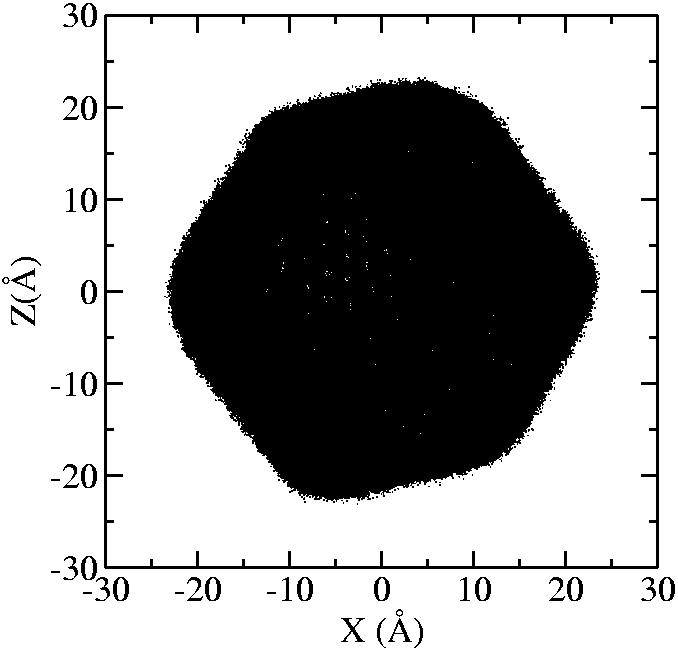
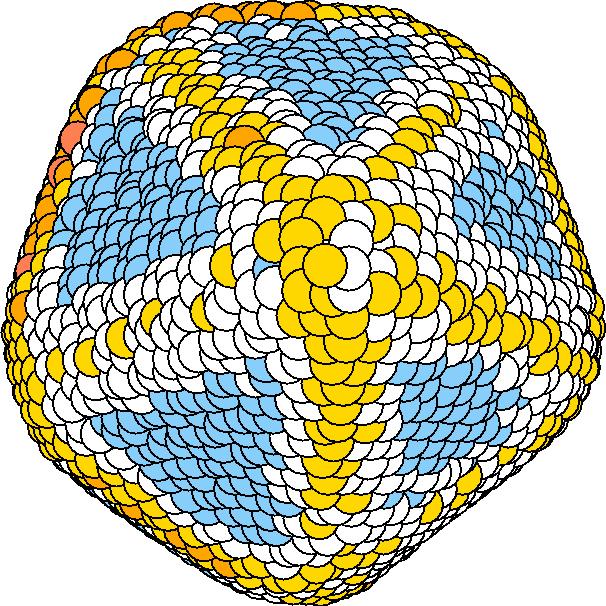
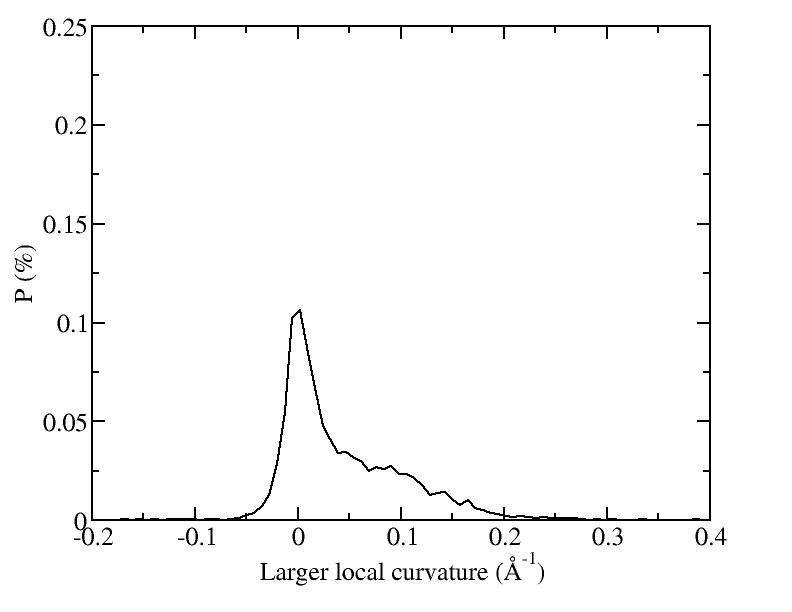
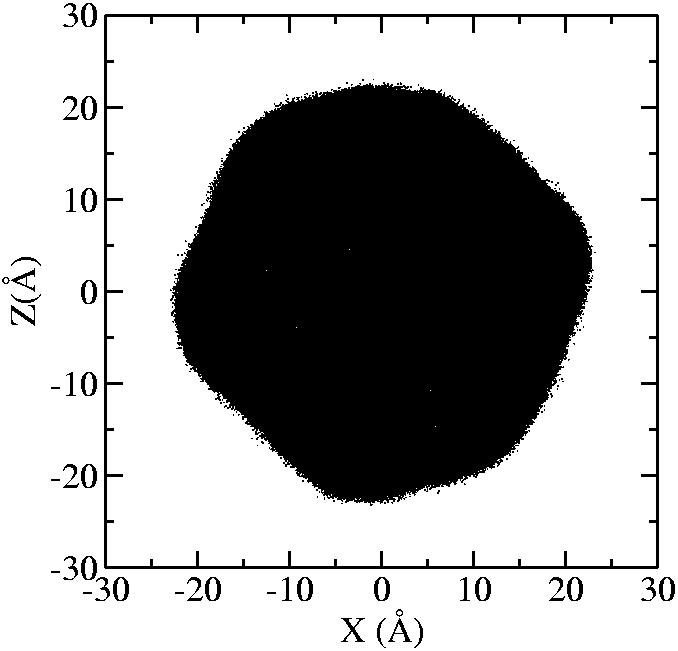
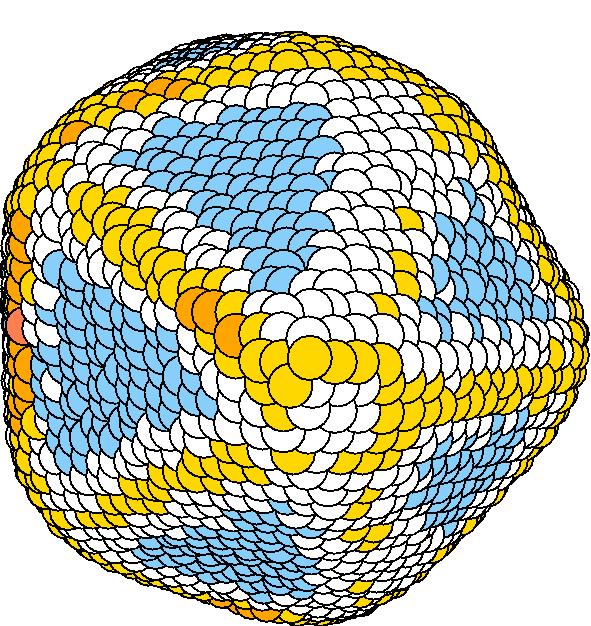
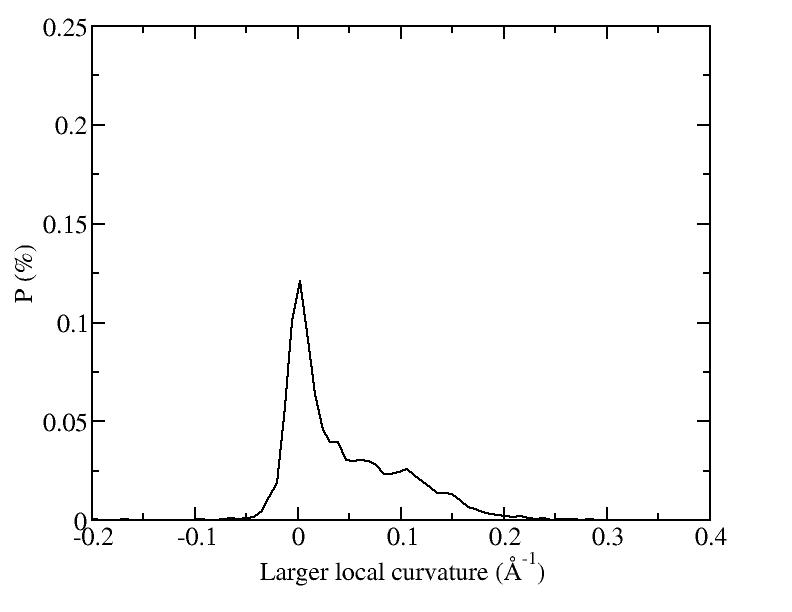
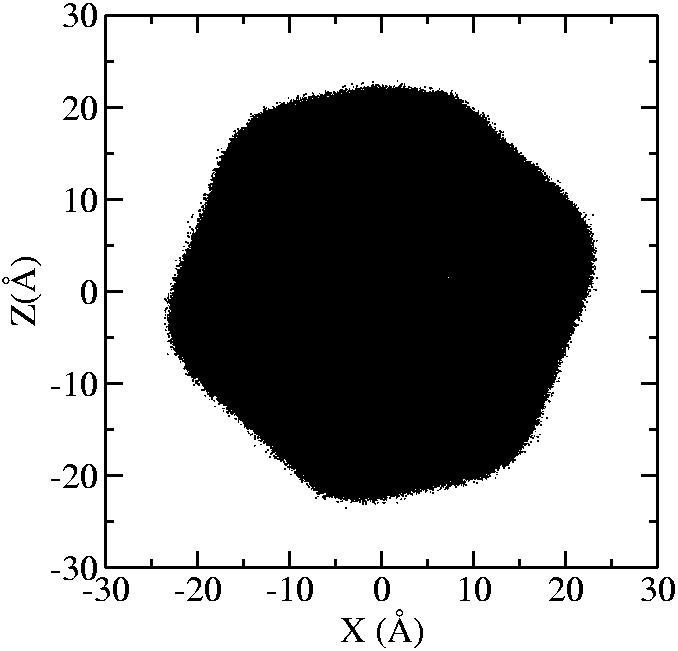
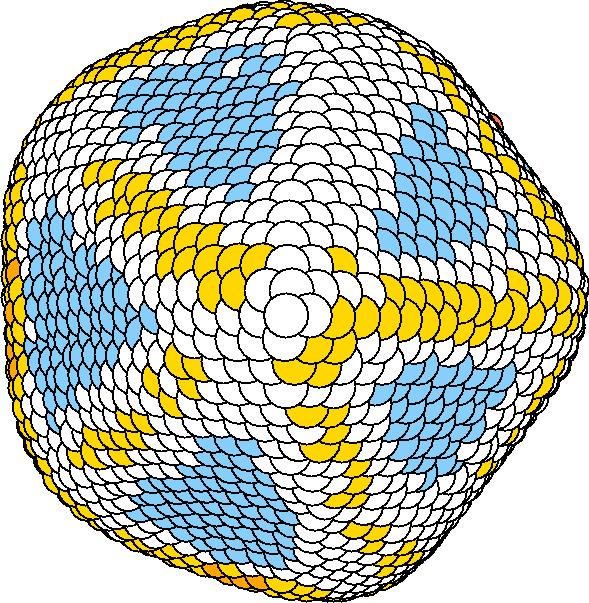
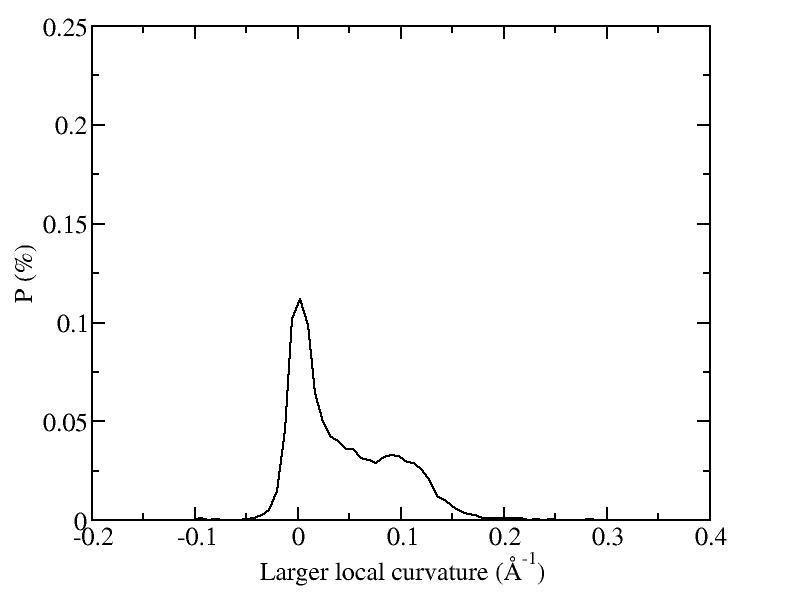
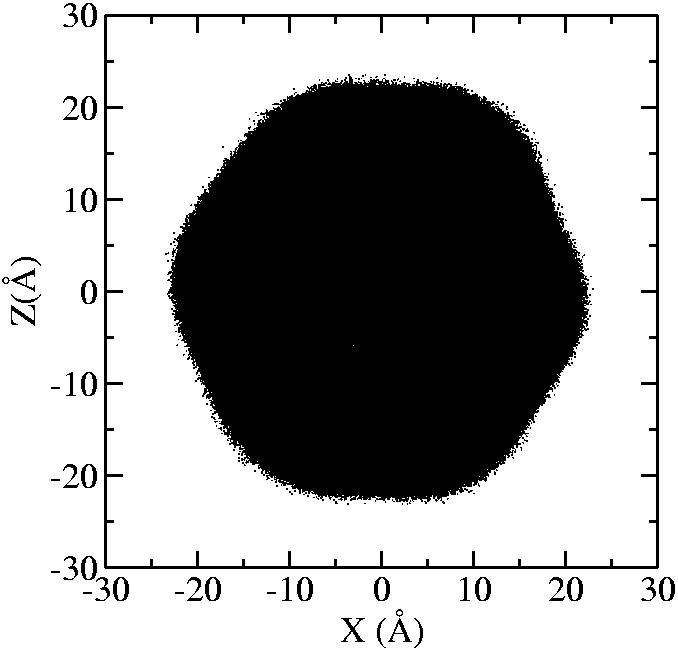
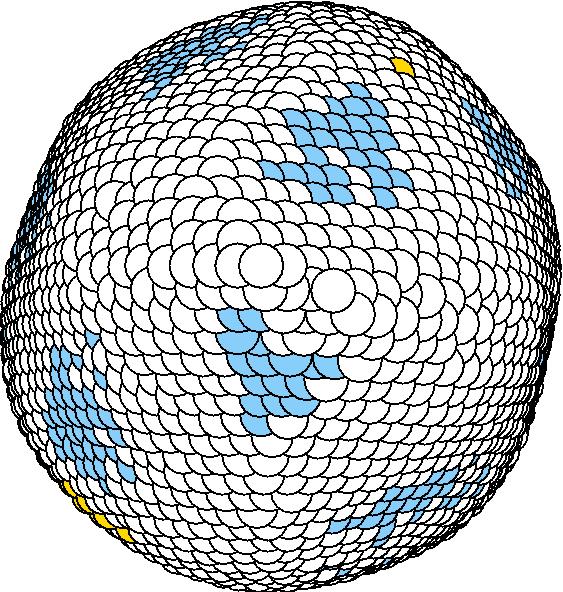
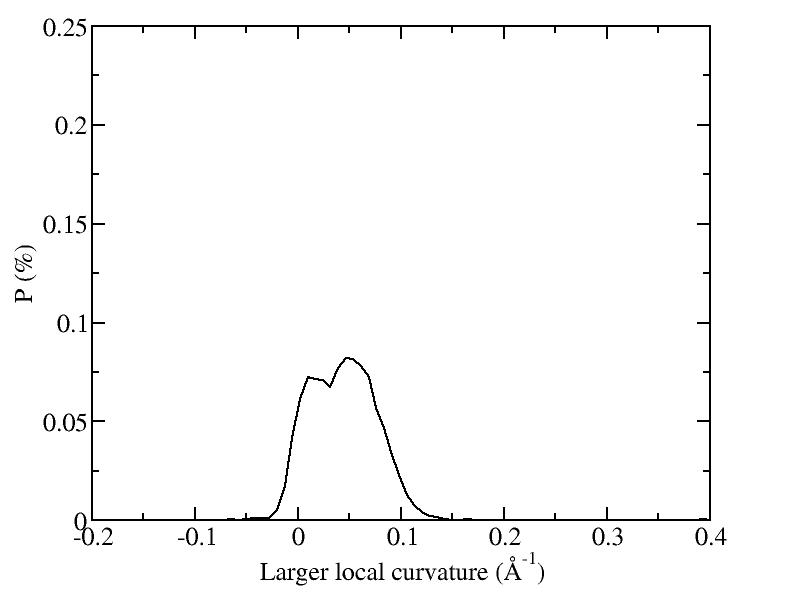
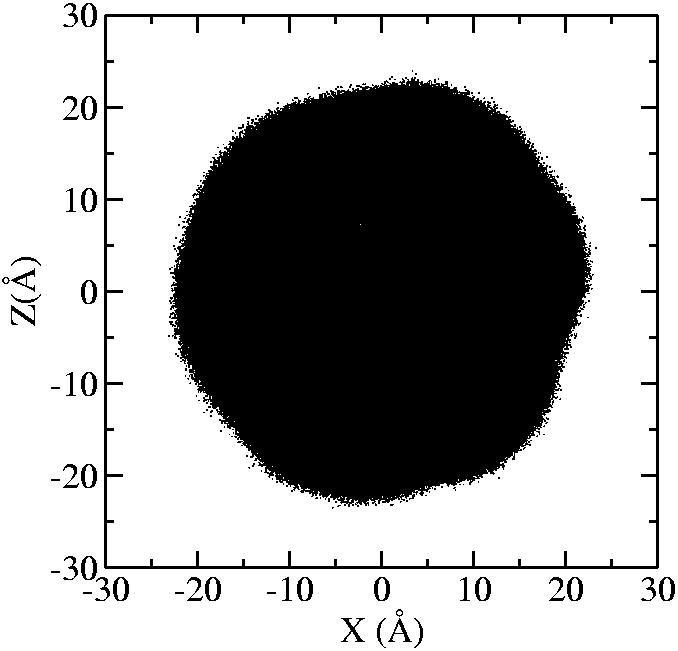
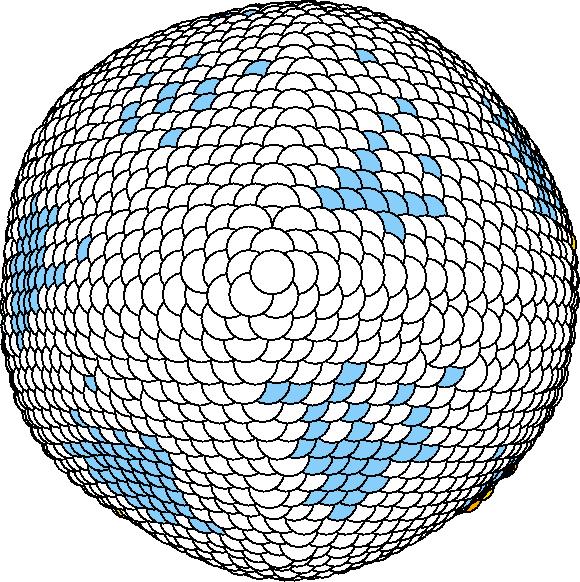
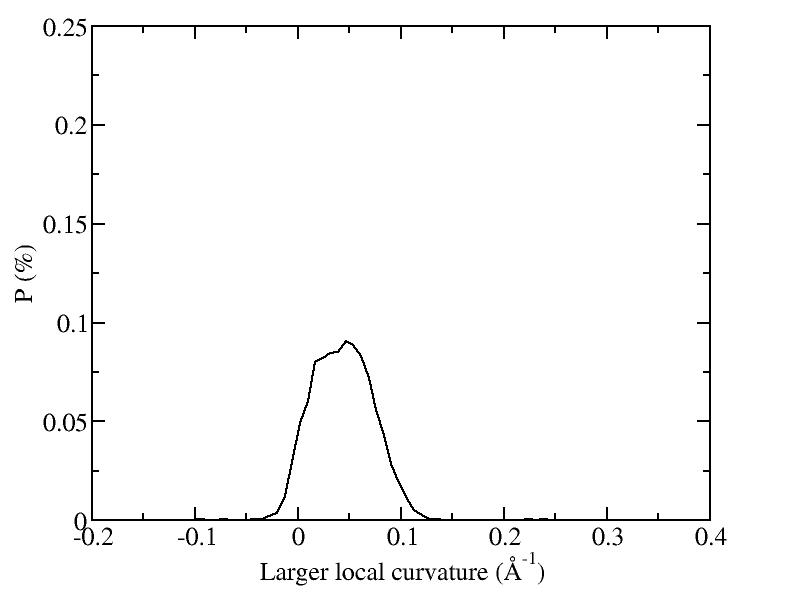
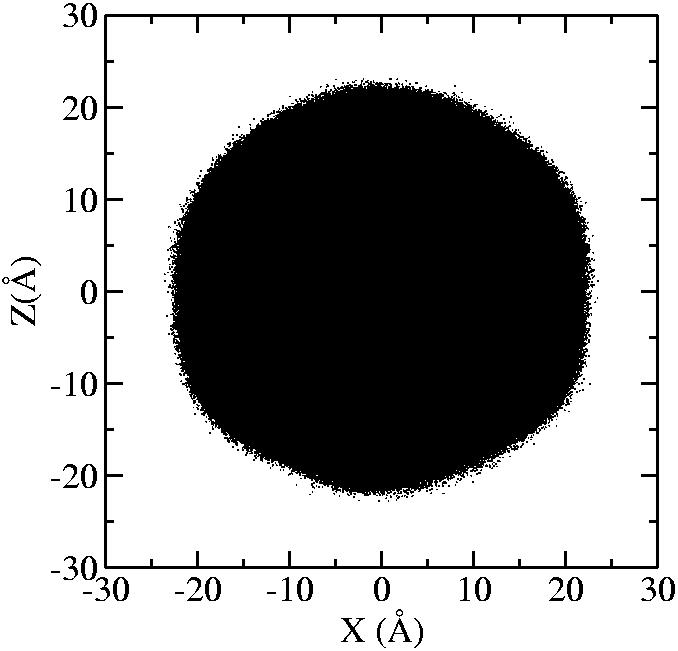
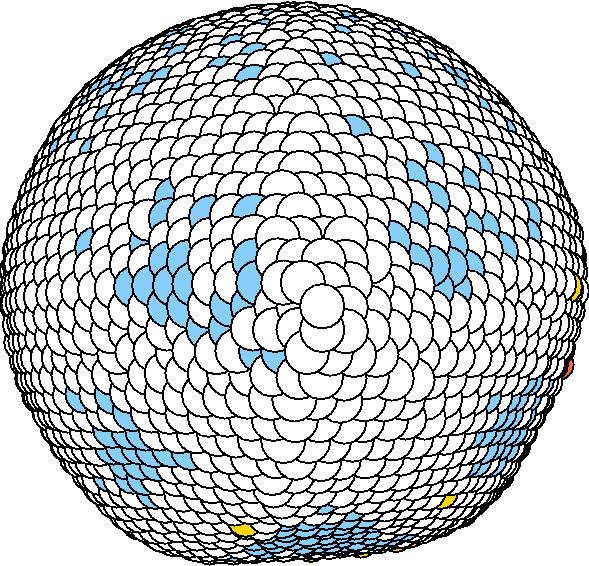
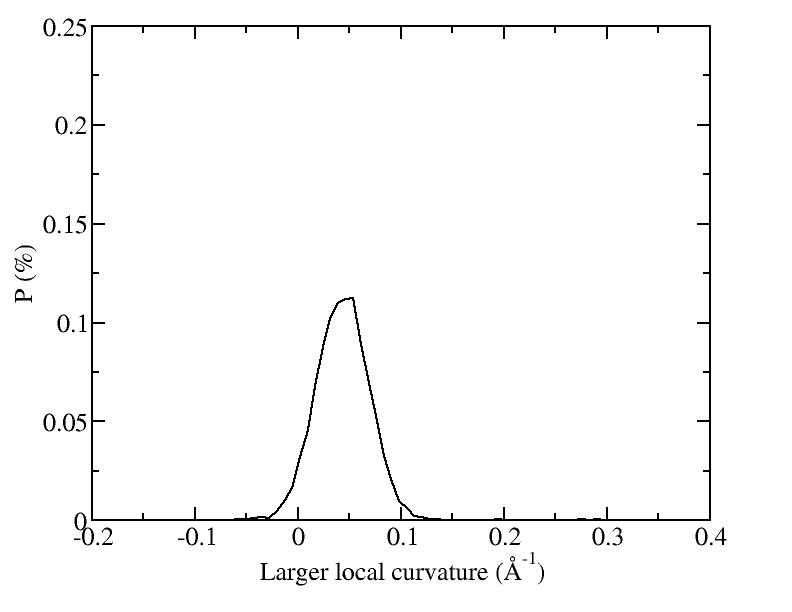
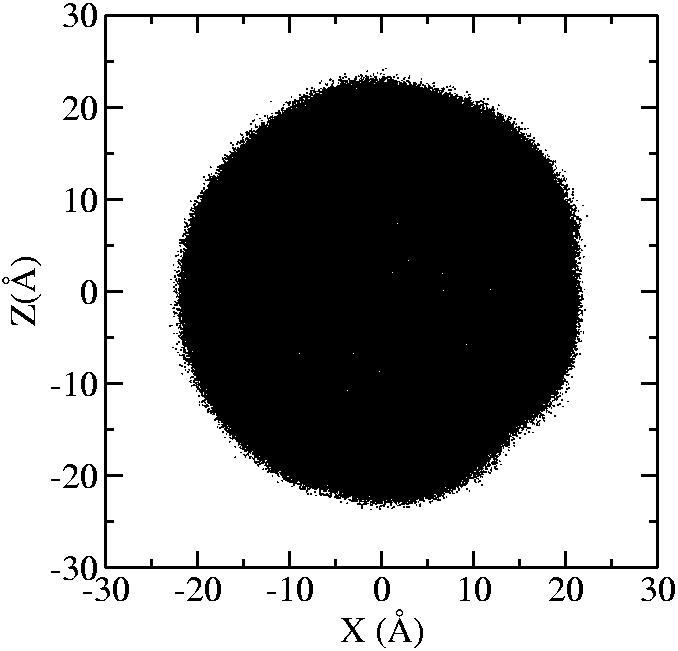
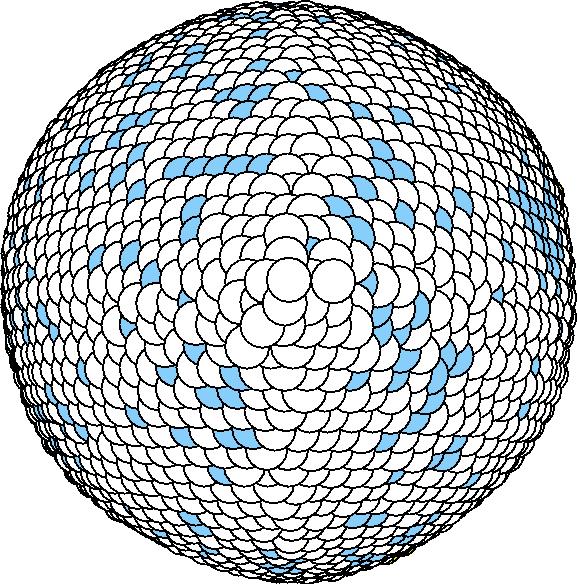
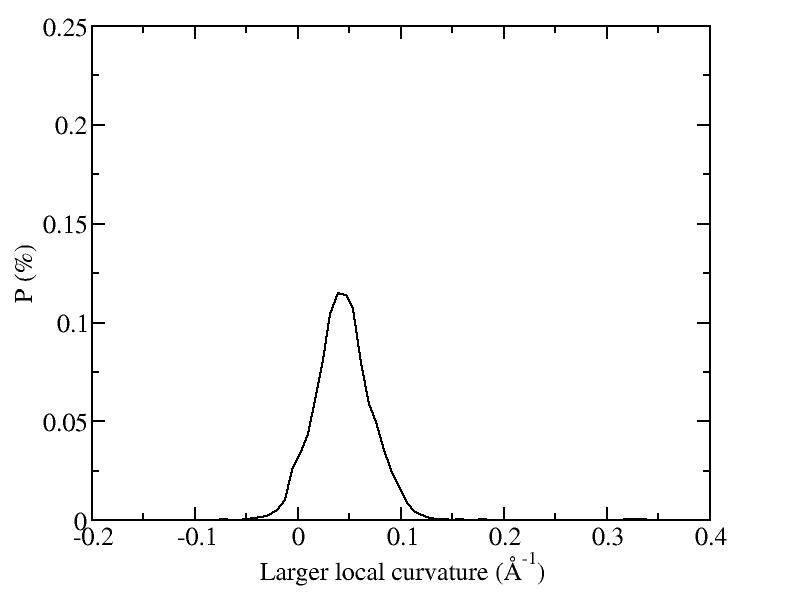
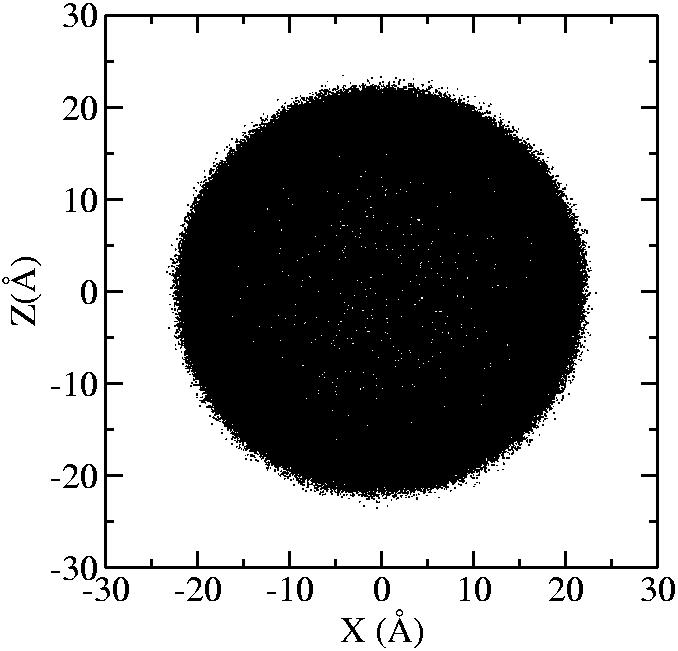
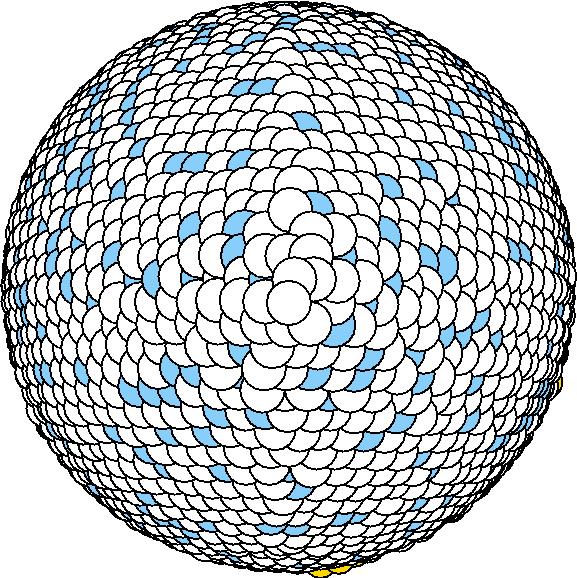
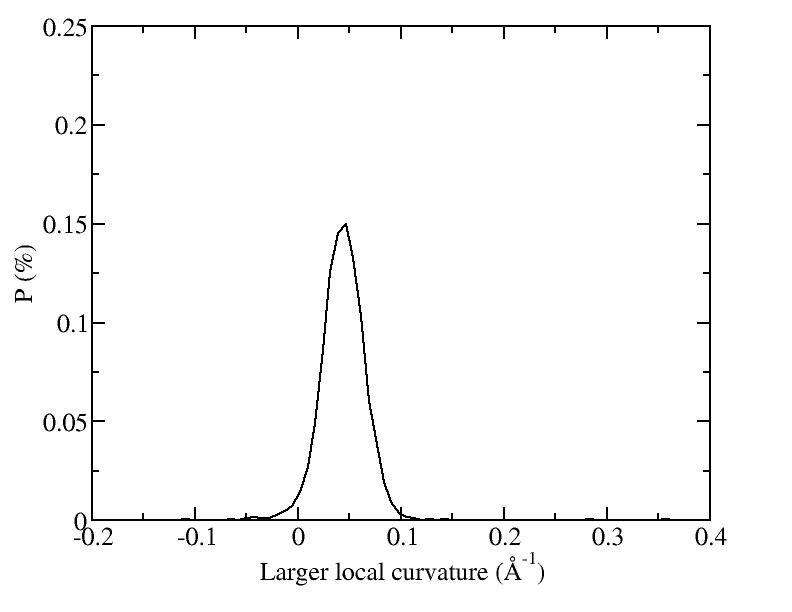
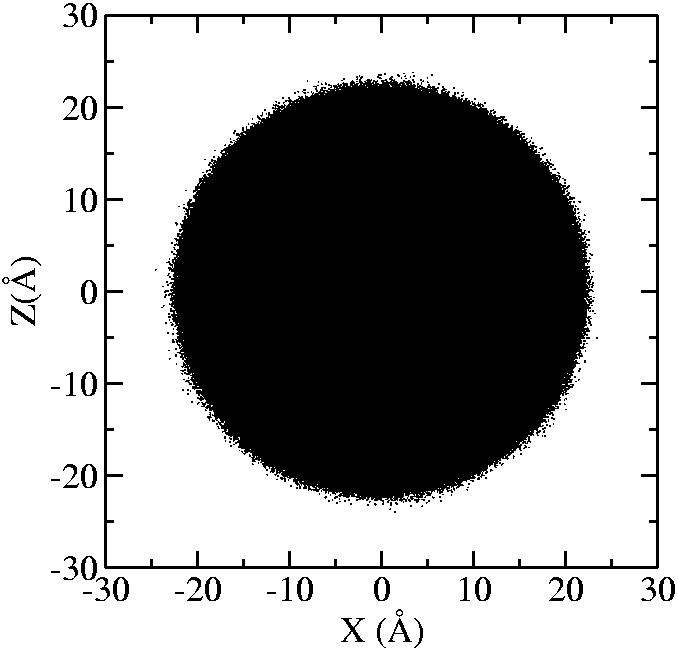
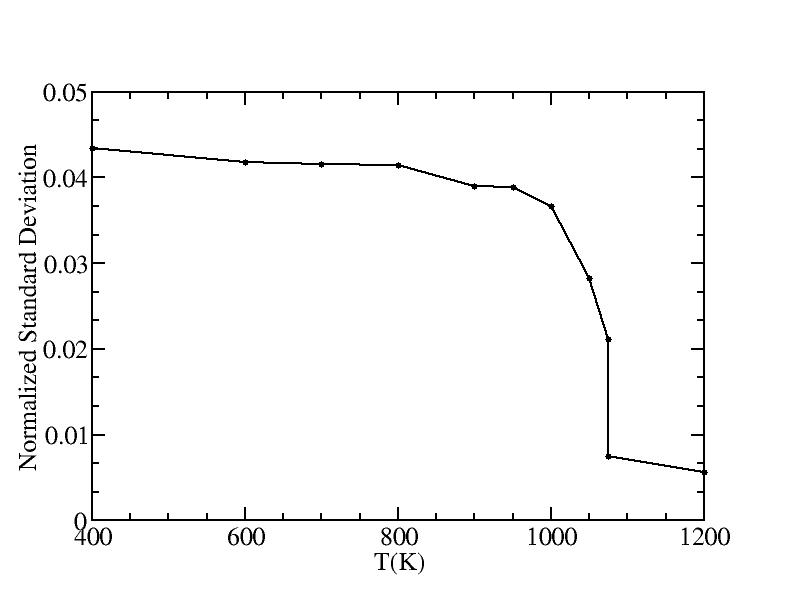
At 1075K, the system keeps solid for 610 configurations and became liquid for 390 configurations. So we treat the two situations seperately as "1075K solid" and "1075K liquid".

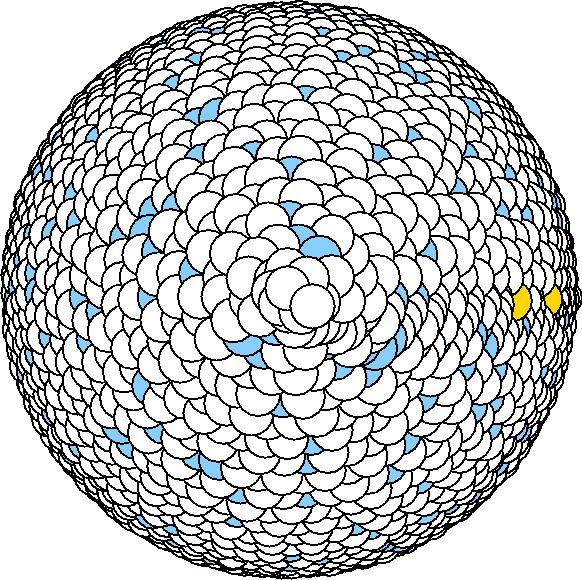
We should average the instantaneous configurations to get the average shape. Averaging the positions of each surface atom, however, is not satisfactory because the atoms diffuse at high temperatures. So we have to find out a method independent to the individual atoms. One way to do it is to divide the spherical space into solid angle cells and average the positions of the surface atoms inside each cell to get one bead for this cell. We divided theta evenly and phi with the weight of Sin(theta). The colored average shapes can be downloaded here.

After we got the average shape, we wanted to quantify "how round" the average shape is. For each average shape, we found the optimized sphere (r_c, R) for it:

R= sqrt( sum_i(r_i - r_c)^2 / N ),

where r_c is the center of mass, R is the radius.

Then we calculated the standard deviation of the distance from the beads to the optimized sphere:

Sd = sqrt( sum_i (|r_i - r_c| - R )^2 / N ) and let it to be the measurement of the "rounding" of the average shapes.

Pictures

Standard deviation of the average shapes

Shape distributions in 2D and average shapes in 3D

T 2D projection 3D average shape Contour plot Larger local curvature distribution

400K

600K

700K

800K

900K

950K

1000K

1050K

1060K

1070K

1075K solid

1075K liquid

1200K

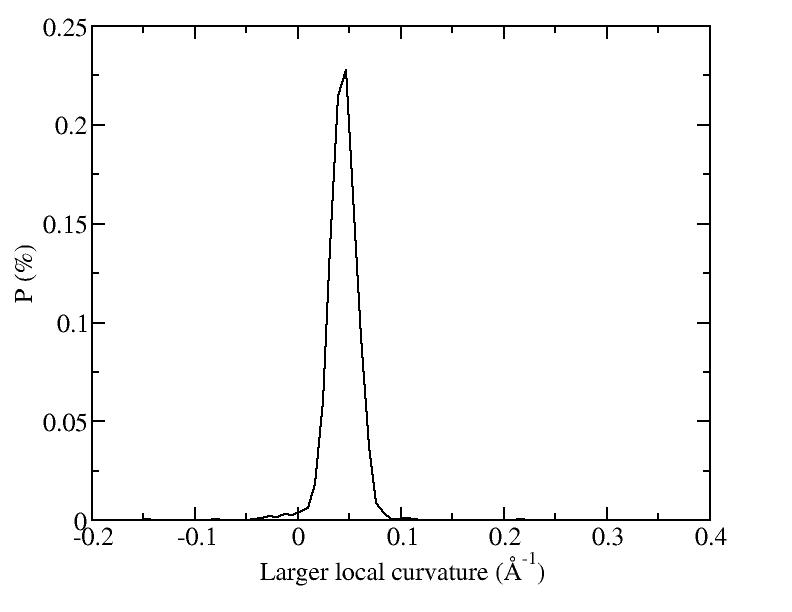
T	2D projection	3D average shape	Contour plot	Larger local curvature distribution
400K
600K
700K
800K
900K
950K
1000K
1050K
1060K
1070K
1075K solid
1075K liquid
1200K