Conservation of Energy
and Angular Momentum

Conservation laws are important because constrain how physical systems change. Hidden in Newton's laws are the conservation of energy, and the conservation of angular momentum. Both of these principles are useful in understanding some of our previous results and are fundamental in physics.

Energy Conservation

In the gravitational physics of orbits that we have been considering there are two important forms of energy that are being exchanged. GRAVITATIONAL POTENTIAL ENERGY and KINETIC ENERGY. The kinetic energy is the energy associated with a object's motion and is given by

Ekin= Mb V2/2.

where Mb is the mass, say of a ball, and V is the magnitude of the velocity (the speed).

Now the gravitational potential energy is the energy that a body has which can subsequently be used to accelerate the body to a larger magnitude of velocity. For example, if I hold a ball at arms length at rest, and let the ball drop to the Earth, the ball will speed up before hitting the Earth. This potential energy, as I was holding the ball at rest, is given by

Egrav=Mbg H,

where H is the height of the ball above the Earth's surface, and g, the acceleration on the Earth is g=(GMe/R2e) = 9.8 meters/s2 (see the inset figure in the discussion of weight on our earlier packet of notes The Universal Law of Gravitation ).

Now here's the deal: the gravitational potential energy of the ball at rest in my extended arm, is equal to the maximum kinetic energy that the ball can have just before it reaches the ground. As the ball falls, H decreases. Thus the gravitational energy decreases. Where does it go? Well, the speed of the ball increases. Thus the kinetic energy of the ball increases from the equation for kinetic energy above. Gravitational potential energy is being converted into kinetic energy. This is how energy is conserved.

It is also why you slow down and speed up as you travel up and down in a roller coaster.

Is it consistent with planets in elliptical orbits around the sun speeding up near the the perihelion and slowing down near the aphelion? and Kepler's second law?

A bit more on the Ball

Back to the ball: note that when I drop the ball, it bounces back up it slows down as its gravitational potential energy is regained. Why does does the ball always return to a height slightly lower than that from which is was originally dropped? The reason is that there are other sources of energy loss: heat, compression, stresses on the ball itself which cannot be regained as gravitational energy. However, when all these energies are added up, their total is equal to the same as the initial gravitational potential energy.

Energy conservation is fundamental. Physics can describe to us only how energy in the Universe transforms from one form to another.

Angular Momentum Conservation

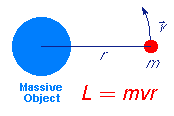Objects executing motion around a point possess a quantity called ANGULAR MOMENTUM. This is an important physical quantity because all experimental evidence indicates that angular momentum is rigorously conserved in our Universe. It can be transferred, but it cannot be created or destroyed. For the simple case of a small mass executing uniform circular motion around a much larger mass (so that we can neglect the effect of the center of mass) the amount of angular momentum takes a simple form. As the adjacent figure illustrates the magnitude of the angular momentum in this case is

L = mvr

where L is the angular momentum, m is the mass of the small object, v is the magnitude of its velocity, and r is the separation between the small and large objects.

Ice Skaters and Angular Momentum

This formula indicates one important physical consequence of angular momentum: because the above formula can be rearranged to give v = L/(mr) and L is a constant for an isolated system, the velocity v and the separation r are inversely correlated. Thus, conservation of angular momentum demands that a decrease in the separation r be accompanied by an increase in the velocity v, and vice versa. This important concept carries over to more complicated systems: generally, for rotating bodies, if their radii decrease they must spin faster in order to conserve angular momentum. This concept is familiar intuitively to the ice skater who spins faster when the arms are drawn in, and slower when the arms are extended; although most ice skaters don't think about it explicitly, this method of spin control is nothing but an invocation of the law of angular momentum conservation.

Notice how this applies to elliptical planetary orbits. For a planet of mass m in an elliptical orbit, conservation of angular momentum implies that as the object moves closer to the sun it speeds up. That is, if r decreases then v must increase to maintain the same L. Thus near perihelion it speeds up and near aphelion it slows down. Both energy conservation and angular momentum conservation are important to planetary orbits.

Hey, wait a minute, why do the planets have any orbital angular momentum?

Note that the reason planets orbit the sun and do not fall into the sun, is because they have angular momentum and have had this angular momentum from the time they were formed. The planets could have gained this angular momentum before or after their formation, but it is believed that they were likely formed from gas material that was already orbiting the Sun. More on this later.