"The Closest Known Flyby of a Star to the Solar System"
Mamajek, E.E., Barenfeld, S.A., Ivanov, V.D., Kniazev, A.Y., Vaisanen, P., Beletsky, Y., & Boffin, H.M.J, 2015, Astrophysical Journal Letters, 800, L17
(see FAQ below)
Links to Astrophysical Journal Letters Article, ArXiv, and UR Press Release (Tuesday 17 February 2015)
Previous studies: Scholz (2014), Burgasser et al. (2015), Ivanov et al. (2015)
SIMBAD entry for Scholz's star | Wikipedia entry
Google Sky .kml file for finding Scholz's
star and showing a best estimate of its trajectory over the past
million years (it's the faint star just above and to the left of
the final pin corresponding to its 2010 position)

Artist's conception of Scholz's star and its brown dwarf companion (foreground) during its flyby of the solar system 70,000 years ago. The Sun (left, background) would have appeared as a brilliant star. The pair is now about 20 light years away. Credit: Michael Osadciw/University of Rochester.
FAQ about Scholz's star (WISE J072003.20-084651.2), which had the
closest known flyby of a star system to the solar system
What do we know about Scholz's star?
Scholz's star was discovered in 2014 by Ralf-Dieter Scholz
(Scholz
(2014)). It is a red dwarf + brown dwarf binary system (spectral
types M9.5 and
T5). Burgasser
et al. (2015) reported the discovery of its brown dwarf companion
in October 2014, and reported precise radial velocity measurements and
an improved distance (6.0 parsecs = 19.6 light years). I estimate the
masses of the two components to be roughly 86 and 65 Jupiter masses
(0.082 and 0.062 times the mass of the Sun). The SIMBAD database
has a
new entry for this recently discovered star, which summarizes its
basic observables.
Why did you nickname WISE J072003.20-084651.2 "Scholz's star"?
The star was first discovered to be a nearby star by astronomer
Ralf-Dieter Scholz of Leibniz-Institut fur Astrophysik Potsdam (AIP)
in Germany. The star was first reported by Scholz in a paper that
appeared on arXiv in
November 2013, and subsequently published
in the
journal Astronomy & Astrophysics in January 2014. The star is
very interesting for multiple reasons: (1) it is a late-M + T dwarf
binary, (2) it was very slow proper motion and was previously missed
as a nearby star, as it was within a couple degrees of the Galactic
equator, and (3) now we know it as the star that came closest to the
solar system in the recent past (although I suspect when all is said
and done after analysis of the Gaia
mission astrometry in the years ahead, probably some other star
will win the prize for having come closest (or coming closest) in the
future). This star is clearly interesting enough that it warranted
some sort of nickname beyond its boring "phone number" designation
(based on its celestial coordinates).
Was Scholz's star "seen" before 2014?
It was an anonymous star that appeared in several star catalogs (it is
also designated as 2MASS J07200325-0846499, DENIS J072003.2-084650,
and USNO-B1.0 0812-00137383 - since it appeared as a source in the
2MASS and DENIS infrared sky surveys and on photographic sky survey
plates in the USNO-B1.0 survey). However there was nothing about the
star that drew astronomer's attention before 2014. To appreciate
just how faint and anonymous it was, check it out in
Google Sky. There are many billions of
stars on the sky that are similarly anonymous - and barely studied
beyond their positions and how bright they are at visual and infrared
bandpasses. Red stars near the Galactic plane are a dime a dozen,
especially slow moving ones like Scholz's star. What stood out was
that it was relatively nearby.
Why was Scholz's star not discovered before 2014? How did it remain
hidden for so long?
A few factors probably contributed to it being missed for so long.
(1) It is very dim at visual wavelengths - 18th magnitude in the
V-band, (2) It is near the Galactic plane (Galactic latitude +2.3
degrees) - so it is in a crowded region of sky, (3) that crowded
region of sky has lots of red stars - but most are red giant stars
that are much, much further away, (4) the star has a low proper motion
(and corresponding tangential velocity) - nearby stars are easier to
find if you search the ones that appear to be fast moving. Scholz's
star is moving fast with respect to the solar system - but most of its
motion is radial (83 km/s), with slow tangential motion
(3 km/s). But to measure a radial velocity, you have to measure a
spectrum to measure the Doppler shift - and one would need the star to
stand out somehow before bothering to take a spectrum. Scholz was the
first to notice that this star was interesting. While the star's
tangential motion is small - it is not zero. He selected it based on
its combination of WISE infrared and 2MASS near-infrared colors - and
the fact that it had moderate proper motion (~0.1 arcsecond per year)
hinted that it was not simply a more distant red giant, but most
likely a nearby red dwarf.
What about HIP 85605 - the "Rogue Star"/"Deadly Dwarf Star"/"Death
Star" that is supposed to wipe out Earth in 240,000 to 470,000
years?
We discuss HIP 85605 in Section 3 of our
paper. Bailer-Jones
(2014) conducted an excellent survey of about 50,000 stars in
the Hipparcos catalog to try to identify cases of stars that came
very close to the solar system (or will in the future). His
closest flyby was for a star HIP 85605 - a previously uninterested
orange (K-type) dwarf. If the revised Hipparcos trigonometric
parallax for HIP 85605 was taken at face value (placing the star
about 7 parsecs of 22 light years away), then the star's
trajectory would bring it to within 0.10 parsec (0.33 light year =
21,000 astronomical units) - near the inner Oort cloud - about
300,000 years in the future. Bailer-Jones discusses the distance
to the star at some length - since it had large uncertainties, and
its astrometric solution may have been affected by another
unrelated neighboring star. Unfortunately, as we show in Mamajek
et al. (2015), the Hipparcos distance to HIP 85605 is almost
certainly wrong - and it is probably about 10x further away than
previously thought. The reason is that the Hipparcos distance
forces the star to have a very dim absolute magnitude (Mv =
11.9+-0.5), much dimmer than plausible for a typical orange dwarf
of the same color (main sequence K dwarf would have Mv of around
7!). So the Hipparcos parallax places HIP 85605 about 5
magnitudes below the main sequence - and in a region of
color-magnitude space where no known stars lie. It would be too
faint to be even a very metal poor orange dwarf, and it is too
bright to be a cool white dwarf. I illustrate this point in a plot
posted
to figshare. Furthermore,
David Latham (CfA) has confirmed that spectra of HIP 85605 taken
over a decade ago do show it to be a typical orange dwarf star. So
the Hipparcos distance is unphysical. At the more likely distance
of ~60 parsecs (nearly 200 light years), the trajectory of the
star doesn't bring it much closer than 10 parsecs (~30 light
years) of the solar system. So we conclude that HIP 85605's close
flyby is probably an artefact of a poor Hipparcos astrometric
solution for HIP 85605. Scholz's star is then currently the record
holder for the nearest known flyby of a star to the solar
system.
So despite the unfortunate headlines from December 2014 about HIP
85605 -
e.g. "Is
a Death Star Coming at US? Study Says It's Possible But Don't
Panic" - I'm very confident that HIP 85605 will not be
making a close flyby of the solar system in the distant future
(triggering a comet shower, etc. etc.).
Is Scholz's star bound to the Sun? i.e. part of our solar system?
No, we're entirely certain Scholz's star is NOT on a bound
orbit with our Sun - it is NOT part of our solar system. It is not in
orbit around the Sun - indeed it appears to have traversed *20 light
years* in about 70,000 years since its "flyby" of the solar
system.
How do we know it was not bound to the Sun? Some observations
and basic Newtonian physics. When it passed ~52,000 AU from the Sun
~70,000 years ago, its velocity was about 83 kilometers per second.
We can easily calculate the escape velocity for a body at that
distance from the Sun using basic Newtonian physics: The escape
velocity of an object is:
V_esc = root(2 G Msun / r)
where "G" is the Newtonian gravitational constant, "M" is the mass of
Sun (really the mass of solar system, but the Sun completely dominates
the first 3 digits anyway), and "r" is the separation between the Sun
and Scholz's star at its minimum flyby separation. G = 6.67-11
m^3/kg/s^2, Msun = 1.99e30 kg, and r = 52,000 AU = 7.8 trillion km =
7.8e15 meters. This translates to an escape velocity of only 185
meters per second (0.185 km/s) at that separation! If Scholz's star
had a velocity lower than this, then it could be on a bound
orbit. But, the velocity of Scholz's star was actually ~450 times
too fast to remain bound to the Sun. So like every other star we
know, it is unbound to the Sun, and merrily going about its business
orbiting the Galaxy. Scholz's star and our solar system were simply
ships passing in the night.
Is Scholz's star actually any of the following hypothetical
objects: "Tyche", "Nemesis", "Nbiru", or [other made-up object
supposed to invoke fear and foreboding, and sell silly new age
books]?
No. "Tyche"
and "Nemesis"
are names attached to particular predictions about hypothetical
companion to the Sun (neither of which has ever been seen and probably
do not exist). Sensitive surveys of the sky in the infrared have ruled
out distant companions to the Sun down to the mass of Jupiter or
Saturn (depending on distance; see WISE survey paper
by Luhman
(2014)). However, given the eccentric orbits of some of the
distant objects many dozens of AU away from the Sun (e.g. Eris, Sedna,
etc.), it wouldn't shock me if a body the size of Mars or Earth were
discovered beyond the Kuiper Belt (but seems unlikely if a giant
planet, brown dwarf, or star will be found in the Oort Cloud).
"Nibiru" is apparently related to some bizarre pseudoscience doomsday
hoax. Needless to say - it's crap, and without the internet to
perpetuate silly ideas, it probably would have died years ago. From
what I've seen on various youtube videos (what passes for scholarship
in the Nibiru-phile community), Nibiru appears to be a meme propogated
by people noticing what appear to be lens flares and reflections
(e.g. "ghost" images, but not ghosts in the sense of Slimmer or
Casper). It seems ridiculous to consider the idea of a large body
orbiting anywhere close to Earth and the other major planets without
the notice of (1) >10,000 professional astronomers worldwide, (2)
>millions of amateur astronomers regularly observing the night sky,
(3) dynamicists that fit the positional data for the major bodies in
the solar system, integrating their orbits (taking into account the
gravitational effects of all the bodies), and (4) thousands of all of
these folks that regularly tweet, facebook, blog, gossip, post their
images and observations, etc.
All of these parties would take great pleasure being the first to
discover a new large planetary body in the solar system, if they had
observations that supported the discovery of such a body! The
orbits of the major planets and satellites are observationally
constrained well enough that
NASA
can land spacecraft on Mars within a couple hundred meters of the original
targe. The orbits were known well enough 25 years ago, that the
Voyager
2 probe passed Neptune within 100 kilometers of its intended
target position. You simply can't hide something as big as an
Earth-like planet orbiting anywhere near the major planets in the
solar system.
Some things to keep in mind: (1) stars pass through the Sun's Oort
cloud "all the time" - about 10 stars every million years(!), however
extremely few are massive or slow-moving enough or come close enough
to produce any significant impact on the comets in the Oort Cloud.
Close flybys of <20,000 AU (<0.1 parsec, <0.3 light year) that pass
through the denser parts of the Oort Cloud (the inner Oort Cloud) are
very rare - with ones whose combination of mass and velocity are
strong enough to greatly perturb the cloud may occur at intervals of
something like once every ~100,000,000 years or ~billion
years, or so. Fortunately, space is a *very* *big* place - there is a
lot of space between the stars - even during these "flybys".
How bright was Scholz's star at its closest? Was it visible to the
naked eye? How intrinsically bright/luminous/massive would it
have had to have been to be visible to the naked eye?
Scholz's star is currently V = 18.3 magnitude at distance 6.0 parsecs,
so it has absolute V magnitude of Mv = 19.4. At its closest distance
of 0.25 parsecs (52,000 AU) it would have been at magnitude V = 11.4
(there is a typo in Sec. 4 of the paper - the predicted V magnitude
should be 11.4, not 10.3). This is roughly 5 magnitudes (factor of
100x) fainter than the faintest naked eye stars. As we mention in the
paper, Scholz's star is a magnetically active M9.5 star - similar
stars have been seen to flare by more than 9 magnitudes (Schmidt et
al. 2014), so it possible that Scholz's star may have occasionally
been a naked eye object for minutes or hours during rare bright flare
events.
At distance 0.25 pc (52,000 AU), for a star to be naked eye with V
magnitude brighter than 6, a star would have to have absolute V
magnitude brighter than Mv ~ 14, roughly corresponding to a main
sequence star of M5 type or hotter (~15% the mass of the Sun).
Does a low tangential velocity of a nearby star suggest it's
likely either coming towards or has already been quite near or in the
solar system? (Couldn't it have a low tangential velocity AND a low
radial velocity, or if that's an unlikely combo, why so?)
A low tangential and low radial velocity would mean the star's
velocity vector is very similar to that of the Sun's. The velocities
of local stars in the solar neighborhood are smeared out over several
tens of kilometers per second in each dimension (3 dimensions: one
towards the Galactic Center "U", towards the direction of Galactic
rotation "V", and towards the north Galactic pole "W"). The smaller
one draws one box in velocity space (e.g. the velocity of
such-and-such star must be within x kilometers/second of such-and-such
velocity) the fewer field stars will satisfy that criterion (unless
the velocity you originally select is close to that of a nearby
stellar cluster or association). So very few stars have velocities
within a few km/s of that of the Sun (i.e. ones that would show both
tiny tangential motions and radial motions). Stars with really tiny
radial velocities and tiny tangential motions may be
scientifically interesting, however, as such velocities are what you'd
expect for "solar siblings" (i.e. stars that would have shared the
Sun's same birth cluster) - but this is getting off topic. Scholz's
star is certainly not such a star, as it is moving ~83 km/s with
respect to the Sun.
How likely is it that Scholz's star could have flared enough to be
occasionally visible 70,000 years ago?
Good question: while cases of late M-type stars with whopping flares
have been recorded (discovered in all-sky surveys), I'm not sure if
there have been long-term surveys of enough late-M-type stars to get a
good statistical answer (I think stars of M9 and M9.5 type were only
discovered for the first time in the 80s or 90s, and then discovered
in more numbers in the 2MASS and Sloan surveys in the 2000s ). What is
seen among the hotter red (M) dwarf stars is that the most energetic
flares are very rare (months, years), and the least energetic flares
occur more
frequently. Schmidt
et al. 2014 reported a whopping flare of a M8 star. Late M-type
stars are faint, so they really haven't been monitored like
hotter/brighter stars have been. In fact the Schmidt paper is an
example of a previously unknown M8 star that was discovered *because
it flared*. The closing statement in Schmidt et al.'s paper tells the
story: "Overall, however, there are not yet sufficient observations
to characterize the flare frequency distribution of M7-M9 dwarfs and
investigate the similarity of their emission mechanisms to those on
more massive M dwarfs." So a good answer to "how often might have
Scholz's star flared brightly enough to be visible?" is "I don't
know". If you held my feet to the fire to make a bet, I'd probably
estimate a frequency of less than once a year. So I would say that
ultracool red dwarf stars like Scholz's star have been to seen
to brighten by factors of ~4000x, and we know spectroscopically that
Scholz's star is magnetically active, so it seems reasonable that it
probably undergoes similar flares.
Also, are there any remaining alternatives to this possibility
that have not been ruled out - could the current motion of Scholz's
star be the result of more recent interactions with other objects for
example?
Extremely unlikely. Space is a big place. Its high velocity is not
unusual for old stars. And if it had been involved in a recent
interaction with another star that was enough to be responsible for
its high speed - then it probably would have had its companion brown
dwarf stripped away. Nothing is physically odd about the velocity of
Scholz's star itself - the only thing odd is that its motion brought
it so close to the solar system in the "recent" past (~70,000 years
ago).
How close does a star have to come into the solar system to
perturb enough to trigger comets coming into the inner solar system?
How close in would this star have had to come and how about for a star
as massive as Proxima Centauri?
The "danger zone" so to speak is apparently within 20,000 AU of the
Sun - the so-called "inner Oort cloud" or "Hills cloud". In 99.999%
of the simulations of the trajectory of Scholz's star passed well
beyond 20,000 AU (only 1 out of 10,000 simulations brought it within
20,000 AU). The likelihood that Scholz's star passed through the
"outer", low-density Oort Cloud (based on the current velocity and
distance data) is about 98%.
The answer to "How close does a star have to come into the solar
system to perturb enough to trigger comets coming into the inner
solar system?" A star within a parsec or so could perturb
"some" comets towards coming into the inner solar system, but there
are fewer comets in the Oort Cloud that far out to perturb. One way
of quantifying this was proposed
by Feng
& Bailer-Jones (2014) -- they scale their results by defining a
proxy indicator of the encounter-induced flux of Oort Cloud comets
as \gamma = (mass of star)/(velocity of star X flyby distance).
Their simulations are suggestive that gamma < 10^-5.3 (Msun * s / km
/ AU) are unlikely to generate an enhancement in the flux of
long-period comets. For all of the simulations, none of them
resulted in an encounter-induced flux of Oort Cloud comets that came
close to generating a significant enhancement in the flux of
long-period comets.
General comments on the Oort cloud: Some reviews on the Oort Cloud can
be found
in Weissman
1996
and Rickman
2014. Based on the number of long-period comets that enter the
inner solar system, I've seen estimates that there are probably
something like ~trillions of comets in the Oort Cloud. The origins of
the Oort cloud have been debated - with older papers suggesting that
these icy bodies were ejected from the solar system during its
formation, however recent papers
(Levison
et
al. 2010, Brasser
et al. 2012) have suggested that interactions with other stars in
the Sun's original birth cluster were part of the story, and indeed
many or most of the Oort cloud comets may have even been "stolen" from
the vicinity of other stars in the Sun's birth cluster. Our paper
summarizes my understanding of the Oort Cloud so far as I was able to
glean from the literature. My understanding is that there are more
comets within the inner Oort Cloud ("Hills cloud") within about 20,000
AU of the Sun (however it probably does not have a particularly hard
boundary).
Nathan
Kaib, author of a
recent Science
paper on the Oort Cloud and the effects of stellar flybys, said in
a recent email: "As you state in your paper, I think the effect [of
the Scholz's star flyby] on the Oort Cloud and LPC [long period comet]
flux will be minimal." Seeing as Nathan does dynamical
simulations of the Oort cloud and comet populations for a living, I
put some weight in his statement.
How long a duration was the star a solar system "resident"?
This was a journalist's question. I guess by "resident", one
could call it a resident as it passed through as a gravitationally
unbound object passing within the Sun's tidal radius. The Sun's tidal
radius (where its gravity dominates that of the Galactic gravitational
potential) is roughly 1.35 parsecs (calculating discussed
in Mamajek
et al. 2013). Scholz's star passed through the Oort Cloud ~70,000
years ago, as close as ~52,000 AU (0.82 light years). These numbers
are approximate due to uncertainties in the distance, proper motion,
and radial velocity of Scholz's star (discussed
in paper).
If one defines the "solar system" using the rather generous definition
of going out to the edge of the Sun's tidal radius - then Scholz's
star spent about ~30,000 years within this radius (between ~56,000 amd
~86,000 years ago). The star was within 100,000 AU (0.48 parsec) of
the Sun for ~10,000 years (between roughly 66,000 and 75,000 years
ago).
How fast was Scholz's star moving across the sky during its flyby?
Where would it have appeared in the sky (even though it would have
normally been too faint to see)?
At its closest, Scholz's star would have been moving across the sky
at an astounding 70 arcseconds per year (it could traverse a full
moon in about 26 years). Compare this to Barnard's star - the star
with the current highest proper motion (~10.7"/year). It would have
passed closest roughly in the direction of Ursa Major (the Big
Dipper) - however the position on the sky where it was the closest
has large uncertainty (roughly +-30 degrees in RA, +-14 degrees in
Declination).
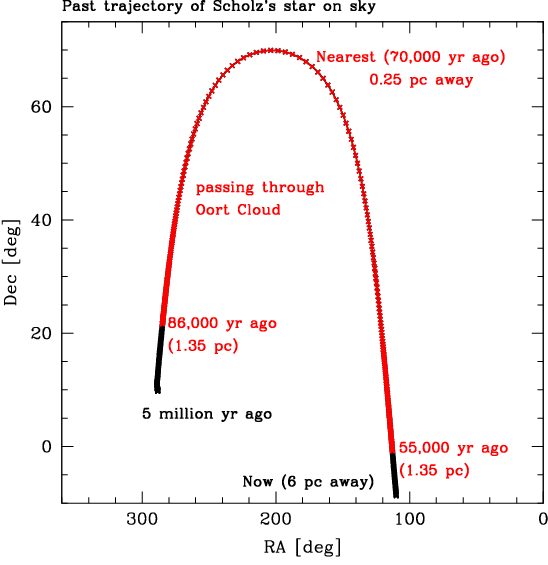
This is a best estimate of the past trajectory for Scholz's star based
on the available velocity and distance measurements. The crosses plot
the star at 100 year intervals - one can see that the angular motion
was much greater near its nearest pass. Its motion is now mostly
radial as it is now moving away (far right, bottom). The red part of
the trajectory shows when the star was within the Sun's tidal radius
(roughly 1.35 parsecs), roughly the maximum possible extent of the
Oort Cloud. Note that 98% of the simulated trajectories brought it
within the outer Oort Cloud.
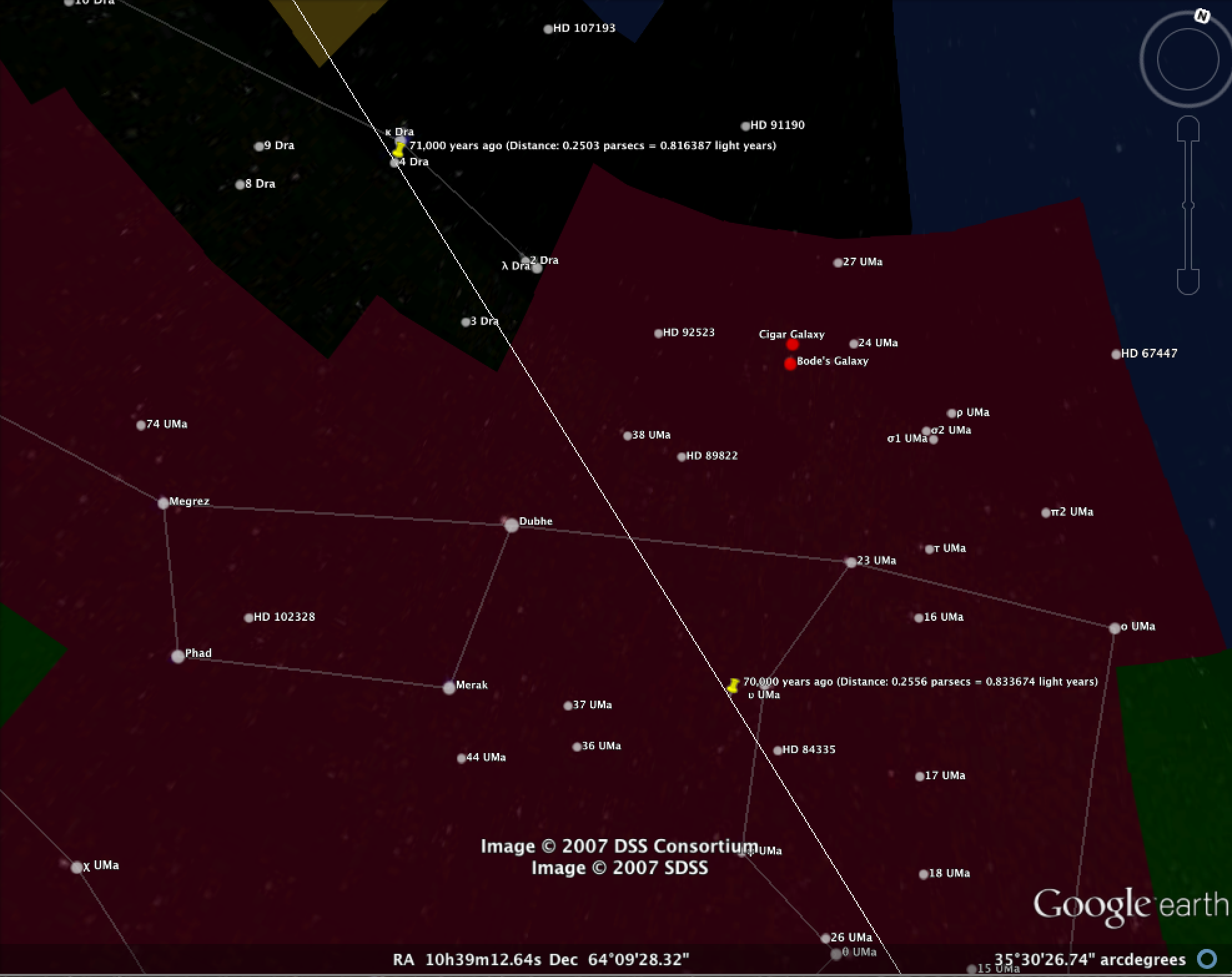
You can also see the trajectory plotted on the sky using this
Google Sky .kml file. Pins are shown at
regular intervals going back 1,000,000 years. Please excuse the extra
significant digits in the calculated distances - those should be
rounded down a bit (indeed the distances are not constrained to better
than ~17% at best, given the current astrometric accuracy). If you
load the .kml file in Google Earth, you can see where the star's
trajectory brought it closest to the solar system. It sailed through
Ursa Major ~70,000 years ago, passing close to the modern position of
the star Dubhe during its closest point. Note that all the
stars are moving. Several of the Big Dipper stars are part of the same
cluster (Ursa Major open cluster) - 70,000 years ago they would have
moved a few degrees but still been in the same general region of the
sky. A Google Sky screen shot of the star's trajectory
through Ursa Major is shown below:
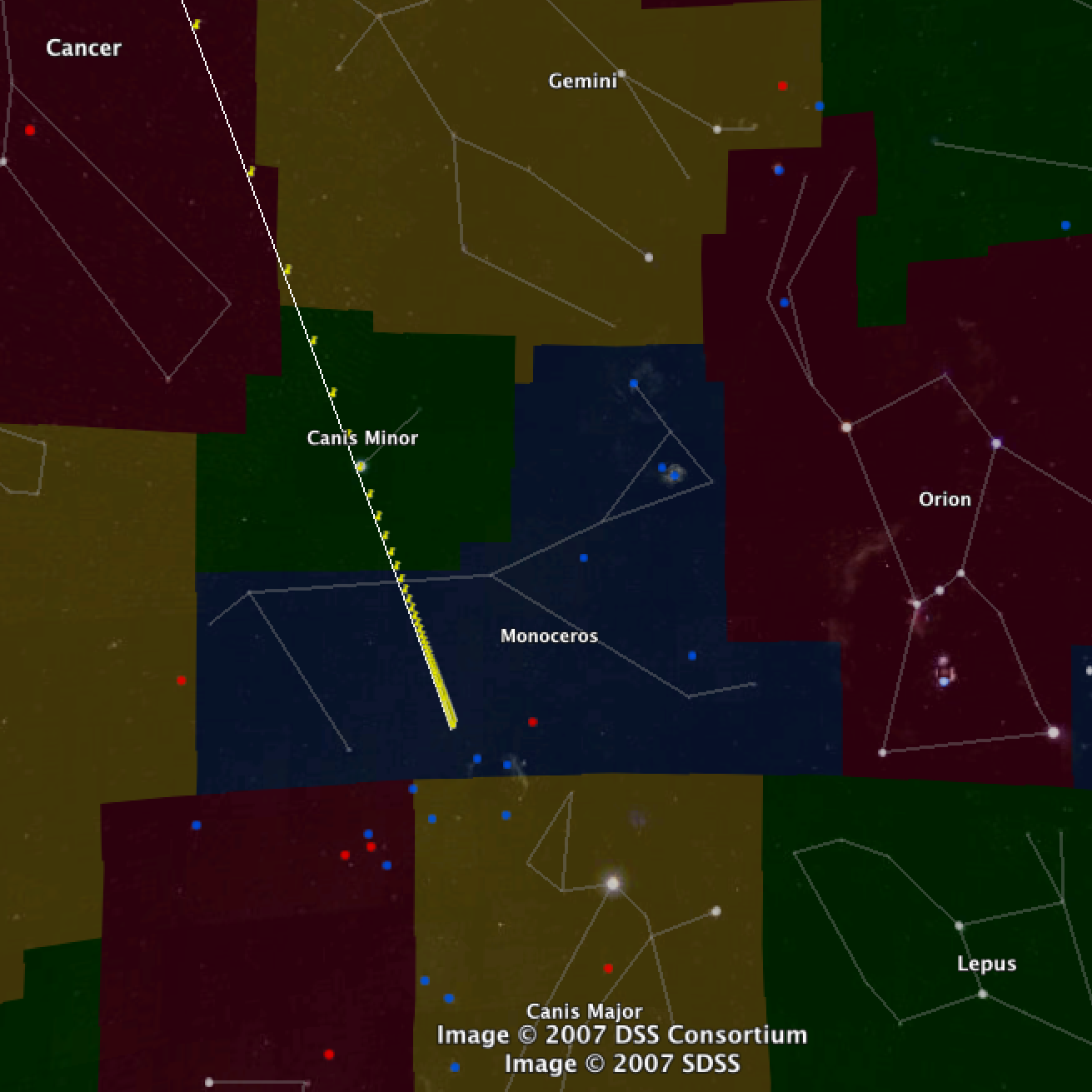
Here is an image from Google Sky showing the past 67,000
years or so of the path of Scholz's star across the
sky (showing it passing through Cancer, Gemini,
Canis Minor, and into Monoceros, where it has spent
the past 55,000 years).
What was the effects of Scholz's star's gravitational
force on the Earth? Its tidal force?
This is a straightforward calculation. Force goes as mass times
acceleration. The acceleration due to gravity goes as:
a = (Gravitational Constant)*(mass)/distance^2
It will be constructive if we calculate this due to Scholz's star at
its closest point, and that for the MOON. Units are in brackets. The
mass of the Scholz's star binary is about 15% the mass of the Sun
(1.99e30 kg) or 3.0e29 kg. Its distance at closest separation was
52,000 AU, where 1 AU is 150 million km (so 7.8e15 meters).
a(Scholz's star) = (6.67e-11)[m^3/kg/s^2]*3.0e29[kg]/(7.8e15[m])^2
a(Scholz's star) = 3.3e-13 m/s^2
And the acceleration due to the Moon? The moon has mass 7.35e22 kg and
it is roughly 384,000 km away.
a(Moon) = (6.67e-11)[m^3/kg/s^2]*7.35e22[kg]/(3.84e8[m])^2
a(Moon) = 3.3e-5 m/s^2
So the ratio of the gravitational accelerations is:
a(Moon)/a(Scholz's*) = 3.3e-5/3.3e-13 = 100,000,000 times!
So the MOON is 100,000,000 x more important gravitationally than
Scholz's star was even at its closest point! The situation is even
more extreme if one compares *tidal* forces, which go as the distance
to the 3rd power!
Let's take the ratio of the tidal accelerations by the moon and
by Scholz's star:
a_tidal(Moon)/a_tidal(Scholz's*) = [(Mass_Moon)/(Mass_Scholz)]*[dist_Scholz^3/dist_Moon^3]
= (7.35e22 kg/3.0e29 kg)*(7.8e15[m])^3/(3.84e8[m])^3
= (2.45e-7)*(8.4e21)
= 2e15 = 2,000,000,000,000,000!
So the tidal acceleration of the MOON on the Earth is 2 QUADRILLION times stronger
than that of the Scholz's star system at its closest point.
The gravitational force and/or acceleration and tidal force and/or acceleration
by Scholz's star on the Earth at its closest point was completely and utterly
negligible compared to nearer smaller objects like the Moon!
Did our solar system pass through the "Oort Cloud" of the
Scholz's binary? Does Scholz's star have a planetary system?
We only know a little about Scholz's star and its brown dwarf at this
point. Scholz's star was only discovered/reported in late 2013 (paper
by Ralf-Dieter Scholz was published early 2014) and its brown dwarf
companion was only discovered by Adam Burgasser et al. in late
2014. In our paper (Mamajek et al. 2015) we estimate the masses of
Scholz's star and its companion - roughly 8.2% and 6.2% the mass of
the Sun (total mass of system ~14.4% of the Sun). The two stars orbit
each other at a separation of about 0.8 AU (Burgasser et
al. 2015). The shape of the brown dwarf's orbit ("B") around Scholz's
star ("A") is not known yet. If we assume a circular orbit, then we
can estimate the size of the regions around these objects where there
may be stable orbits where planets could exist. Following the orbital
stability simulations of Holman & Weigert (1999), these numbers
translate to a region about 0.37 AU in radius around "A" where stable
planetary orbits may exist. The stable zone around "B" is slightly
smaller. There could also be objects that orbit *both* A and B, if
they are situated >1.3 AU away from the center-of-mass for the system.
But these numbers depend on the eccentricity of B's orbit around
A. Given the low-mass of both objects - and based on what we know
about circumstellar disks and the types of planets being discovered
around red dwarfs, if there are planets in the Scholz system, they are
likely small (i.e. unlikely to be gas giants, but there could be ice
giants or smaller rocky or icy planets). Who knows, maybe future
Doppler spectroscopy surveys will be able to detect planetary
companions around Scholz's star?
Why is Scholz's star moving so fast?
Probably because it is a somewhat older star. Its velocity with
respect to the Sun (about 80 km/s) is not that unusual for an "old
thin disk star". Stars in our Milky Way galaxy are generally
classified by their chemical composition, age, and kinematics/velocity
into three rough categories: "thin disk", "thick disk", and "halo" (in
approximate order of age, with "halo" being the oldest
population). The Sun is a medium-aged (~5 billion years) "thin disk"
star. Scholz's star appears to be a "thin disk", but probably somewhat
older than the Sun given its higher velocity. There are stars that
move way faster than Scholz's star that are still bound to our Milky
Way. A good famous example
is Barnard's
star, a nearby ~10 billion-year-old metal-poor star, which is
moving at ~140 km/sec with respect to the Sun.
As mentioned previously, the interaction between Scholz's star
and the Sun was very light. Scholz's star probably "sped up"
by about 0.2 km/sec as it got within a light year of the
Sun, but then decreased its speed by the same amount as
it sped away from the Sun's gravitational field.
Long story short: there is nothing magical about the velocity
of Scholz's star - stars in the solar neighborhood tend to
have velocities that differ from that of the Sun by tens of km/sec,
and sometimes over 100 km/s. But the velocity of Scholz's star
is not that unusual compared to other stars.
Back



