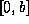 : If
then a closed trapped surface
: If
then a closed trapped surface 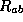 in
in 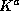 cannot
intersect
cannot
intersect 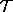 , i.e. cannot be
seen from
, i.e. cannot be
seen from 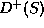 .
.
This section is about two other propositions of the Hawking & Ellis book [3, p 311, p320,].
Proposition 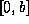 : If
then a closed trapped surface
: If
then a closed trapped surface 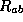 in
in 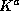 cannot
intersect
cannot
intersect 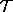 , i.e. cannot be
seen from
, i.e. cannot be
seen from 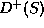 .
.
This demonstration is constructed in the same way the preceeding theorem but is more what we need for the topological censorship and the application to black holes.
The beginning of the proof of that theorem needs to be
explained. First let us define what is meant by 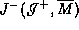
We can embed the spacetime M in a conformal space 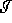 and then glue the boundary
and then glue the boundary 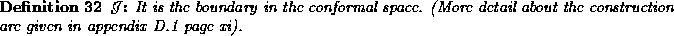 on it.
on it.
This gives us  globally hyperbolic .
It has a Cauchy slice such that it match with the partial
Cauchy slice on M.
globally hyperbolic .
It has a Cauchy slice such that it match with the partial
Cauchy slice on M.
This is a difficult demonstration but it is more general than the restriction of asking for a Cauchy slice. For simplicity let's assume we have a Cauchy slice (like in the Topological Censorship ).
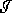
Figure: Representation of the neighborhood of the boundary in one of
the asymptotically flat regions. the rest of the spacetime is not
represented here.
We take the neighborhood of the boundary as on the figure
![]() . Then the causal past of the trapped surface
is a compact region!
The generator intersects
. Then the causal past of the trapped surface
is a compact region!
The generator intersects  so the generator of
so the generator of
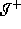 would leave
would leave 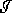 (we
eliminate the case that it hit
(we
eliminate the case that it hit 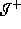 ).
).
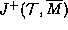 is a null surface because we made the hypotheses
that the spacetime was asymptotically flat and empty.
is a null surface because we made the hypotheses
that the spacetime was asymptotically flat and empty.
We take a null generator, 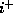 , of
, of 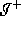 . If it hit
. If it hit 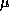 it has an infinite
length but, like we said before, we must have a conjugate
point. So it could not remain in
it has an infinite
length but, like we said before, we must have a conjugate
point. So it could not remain in 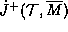 all way out to
all way out to 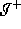 . Therefore
. Therefore 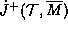 does not intersect
does not intersect 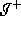 .
.
The difficult part of the proof is to show that 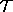 intersects
intersects 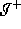 , after it the contradiction
follow easily from what we did before.
, after it the contradiction
follow easily from what we did before.
The fact we take a full Cauchy surface is not a problem
because we add a part of the spacetime which is not causally
linked with the one we study. It cannot influence what we are
doing.
Proposition 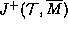 has a similar demonstration. It states
Let
has a similar demonstration. It states
Let 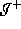 be a regular predictable space developing from a
partial Cauchy surface S, in which
be a regular predictable space developing from a
partial Cauchy surface S, in which  for any null vector
for any null vector 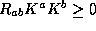 . Then an outer trapped surface P
in
. Then an outer trapped surface P
in 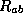 does not intersect
does not intersect 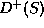 .
.
This kind of demonstration through point set topology will be used in the topological censorship for the lemma 2. The aim of this part was to understand this rather general method which can also be used to generalize to cosmology the Censorship theorem.