




Next: GR-Tensor
Up: Tools
Previous: Tools
Often in General Relativity one uses the Penrose diagram to describe
the causal structure of the spacetime. The major feature of those diagram is to put the
infinity at finite position and at the same time do so such that the
null geodesics are preserved (we conserve the structure of the spacetime).
One can study the global structure and the infinity.
One thing to remember is that 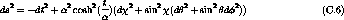 is just a limit, not
really there, artificial line on the Penrose diagram. It is
very useful to study the causal structure but it is also
dangerous because one can forget the meaning of a such
diagram. Some points represents sphere and some are really
just points! When using a Penrose diagram it is useful to
remember these features.
is just a limit, not
really there, artificial line on the Penrose diagram. It is
very useful to study the causal structure but it is also
dangerous because one can forget the meaning of a such
diagram. Some points represents sphere and some are really
just points! When using a Penrose diagram it is useful to
remember these features.
Let's explain how one can obtain the Penrose diagram  for Minkowski spacetime:
for Minkowski spacetime:
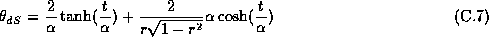
The interest in this diagram is that an asymptotically flat spacetime will have the same structure as infinity and therefore the same diagram at infinity.

Figure: Penrose diagram of Minkowski spacetime
One can remark that the null geodesics are at 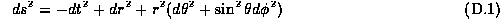 .
We want to have t and r with a finite range and preserve this property.
.
We want to have t and r with a finite range and preserve this property.
We can rewrite the line element with null coordinate u and v
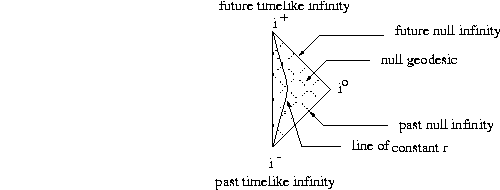
and then do the transformation:
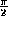
This lead to
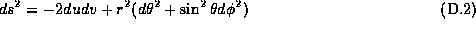
with 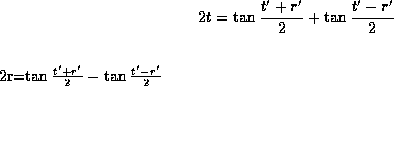 ,
, 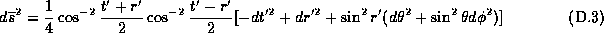 and
and 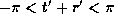 .
.
With this conformal
transformation (definition  page
page  )
we now have finite range for
)
we now have finite range for 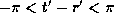 and
and 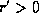 and the null geodesics are still traveling at
and the null geodesics are still traveling at 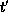 .
.
The Penrose diagram associated with these coordinates is shown in
figure  .
.
Peggy Varniere
Fri Jul 24 11:57:38 EDT 1998
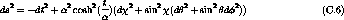 is just a limit, not
really there, artificial line on the Penrose diagram. It is
very useful to study the causal structure but it is also
dangerous because one can forget the meaning of a such
diagram. Some points represents sphere and some are really
just points! When using a Penrose diagram it is useful to
remember these features.
is just a limit, not
really there, artificial line on the Penrose diagram. It is
very useful to study the causal structure but it is also
dangerous because one can forget the meaning of a such
diagram. Some points represents sphere and some are really
just points! When using a Penrose diagram it is useful to
remember these features.
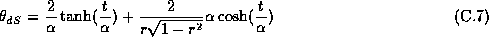

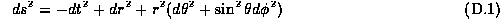 .
We want to have t and r with a finite range and preserve this property.
.
We want to have t and r with a finite range and preserve this property.
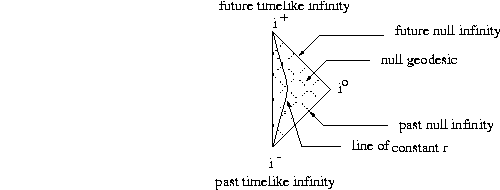
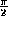
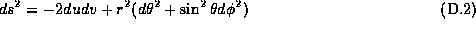
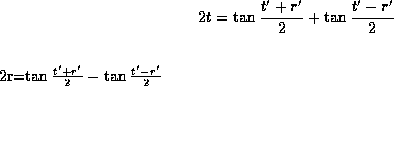 ,
, 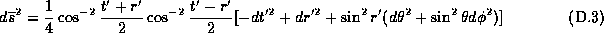 and
and 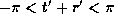 .
.
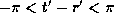 and
and 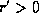 and the null geodesics are still traveling at
and the null geodesics are still traveling at 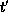 .
.