- Problem 1 [10 points]
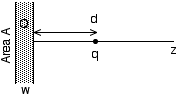
Consider a point charge q a distance d in front of a plane conducting slab of thickness w, as shown below. The slab has a fixed net charge Q on it. Find the electric field on both sides of the slab. Find the force between the charge q and the slab. For this problem, assume that the side area of the slab A is finite, so that the average surface charge Q/2A is finite; however you make work the problem out ignoring edge effects, i.e. assuming the plane is effectively infinite.
- Problem 2 [15 points]
A line charge λ is placed parallel to, and a distance R away from, the axis of a conducting cylinder of radius b that is held at fixed voltage such that the potential vanishes at infinity. Find
a) the magnitude and position of the image charge(s)
b) the potential at any point (expressed in polar coordinates with the origin at the axis of the cylinder and the direction from the origin to the line charge as the x axis)
c) the induced surface charge density, and plot it as a function of angle for R/b = 2 and 4 in units of λ/2πb
d) the force on the line charge per unit length
- Problem 3 [10 points]
A surface charge density σ(φ) = a sin(5φ) is glued over the surface of an infinite cylinder of radius R (φ is the polar angle).
a) Find the potential for r<R inside the cylinder.
b) Find the potential for r>R outside the cylinder.
- Problem 4 [15 points]
Two concentric spherical shells of radii R1 and R2, with R1<R2, are fixed with the following values of the electrostatic potential:
φ(R1, θ) = φ1cosθ and
φ(R2, θ) = φ2
where φ1 and φ2 are constants and θ is the usual azimuthal spherical angle. Find the electrostatic potential for:
a) r<R1, inside the inner shell
b) r>R2, outside the outer shell
c) R1<r<R2, between the two shells
d) Find the surface charge density σ(θ) on each of the two shells.