|
|

Home
Contact
Info
Course
Info
Calendar
Homework
Lecture
Notes
|
|
|
|
Physics 418: Statistical Mechanics I
Prof. S. Teitel stte@pas.rochester.edu ----- Spring 2005
Problem Set 2
Due Friday, February 18 noon, in my mailbox outside the physics department main office
- Problem 1 [15 points]
Consider a box of volume V. The box is split
exactly in half by a thermally conducting
imovable wall. Equal quantities of the same
type of ideal gas fill each half of the box,
and the system is in equilibrium. The total
energy of the gas is fixed at ET.
a) Show that the pressure of the gas on each side is the same.
b) Using the formular derived in lecture for the number of states
of an ideal gas at energy E, 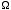 (E), find the
most likely value for the energy of the gas on one side of
the box. (E), find the
most likely value for the energy of the gas on one side of
the box.
c) Using 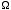 (E), if P(E) is the probability
distribution for the gas on one side of the box to have
energy E, show that the relative width (i.e. the width divided
by the average) of P(E) is proportional
to 1/N1/2, for sufficiently large N, where N is the
number of particles in the gas. This shows that the fluctuation
of E away from its average becomes negligibly small in the
thermodynamic limit of N going to infinity. (E), if P(E) is the probability
distribution for the gas on one side of the box to have
energy E, show that the relative width (i.e. the width divided
by the average) of P(E) is proportional
to 1/N1/2, for sufficiently large N, where N is the
number of particles in the gas. This shows that the fluctuation
of E away from its average becomes negligibly small in the
thermodynamic limit of N going to infinity.
- Problem 2 [15 points]
Consider a system of N distinguishable non-interacting
objects, each of which can be in one of two possible states,
"up" and "down", with energies +e and -e. Assume that N is large.
(a) Working in the microcanonical ensemble, find the entropy
of the system S(E, N) as a function of fixed total energy E and number N (Hint: it
is useful to consider the numbers N+ and N- of up and
down objects).
(b) Find the temperature T as a function of energy E and number N. Show
that T will be negative if E>0.
(c) What happens if such a system (1) with T1<0 comes into thermal
contact with another such system (2) with T2>0? Does T1
increase or decrease? Does T2 increase or decrease? In
which direction does the heat flow?
|

