Problem 1 [10 points]
Consider the same situation as in problem 2, set 2:
A system has N distinguishable non-interacting objects, each of which can be in one of two possible states, "up" and "down", with energies +e and -e. Assume that N is large. Now solve this problem using the canonical ensemble!
a) Working in the canonical ensemble, find the Helmholtz free energy A(T, N) as a function of temperature T and number N.
b) By making the appropriate transformations on A(T, N), find the canonical entropy as a function of the average total energy E and number N. Show that your result, as N goes to infinity, agrees with the entropy you found in Problem Set 2 using the microcanonical ensemble.
Problem 2 [20 points]
Consider a gas on non-interacting, indistinguishable, non-relativistic point particles.
Start with the N particle canonical partition function that we derived in lecture, in which the temperature T, volume V, and number of particle N of the gas are fixed.
a) Suppose now that you wish to describe this gas by a new ensemble in which the pressure p is fixed, and the volume V is allowed to fluctuate. Compute the partition function Z(T, p, N) of the gas in this new constant pressure ensemble (part of this problem is understanding how to define this new ensemble!).
b) If you defined Z properly in part (a), then the Gibbs free energy should be given by
G(T, p, N) = -kBT ln Z(T, p, N)
To demonstrate this, show that using G defined from Z above, the average volume of the system is correctly given by,
<V> = (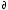
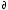G/p)T,N
c) Using G(T,p,N) from part (b), compute the specific heat at constant pressure, Cp, and show that you get the correct answer for the ideal gas.
d) Derive a relation, in this constant pressure ensemble, between the isothermal compressibility 
T and fluctuations in the volume V of the system.
Problem 3 [20 points]
This problem is meant to get you to think about the relationship
between different ensembles and their corresponding free energies,
and how one can often change ensembles to remove a constraint and
make a calculation simpler.
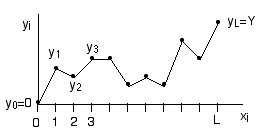
Consider the following model for an elastic string in a plane. The height
of the string at position x is the function y(x). To make the calculation
doable, imagine discretizing the horizontal axis into L discrete units,
xi=i, i=0, 1, 2, ..., L. The height at position xi
is then yi.
The energy to stretch the string is then determined by the
height differences according to the following Hamiltonian:
| H[yi] |
= |
 |  |
L
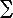
i=1 |
(yi - yi-1)2 |
a) The string is constrained so that its endpoints are fixed at:
y0=0, yL=Y
so that the string has an average slope Y/L.
Compute the partition function
| Z(Y) | = ( |
L-1
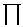
i=1 |
+
- | dyi) e-H[yi]/kBT |
Compute the corresponding free energy,
F(Y) = - kBT ln Z(Y)
There are two tricks you need to sum the partition
function. One is to figure out how to deal with the fact that
yi interacts with both yi+1 and
yi-1. The second is to figure out how to deal
with the constraint of the fixed enpoints. If you get desparate,
here is a hint.
b) Now consider the partition function in a new ensemble
Z'( ) = | +
- |
dY Z(Y) e- Y/kBT |
Z'() is the Laplace transform of Z(Y).
In this ensemble, the average slope of the string, (yL-y0)/L is no longer fixed, but fluctuates. Its average value, however, is determined by the parameter .
Compute the corresponding free energy
F'() = -kBT ln Z'()
Show that the average height difference of the endpoints, Y=yL-y0, is given by
Now take the Legendre transform of F'() to get,
F(Y) = F'() - Y
Show that F(Y) above agrees with what you found in part (a), provided you
take the thermodynamic limit of L -> . That is, show that
the free energies per unit length, F(Y)/L, are equal as L -> .
You should find that the calculation in (b) is much easier and more straight forward to do than the
calculation in (a). This shows that by going to the new ensemble, in which the original constraint of fixed Y was lifted
by introducing its conjugate variable ,
the calculation of F(Y) becomes much easier.
