Home

Contact
Info

Course
Info

Calendar

Homework

Lecture
Notes

Physics 418: Statistical Mechanics I
Prof. S. Teitel stte@pas.rochester.edu ----- Spring 2005

Problem Set 4

Due Tuesday, March 15, in lecture

• Problem 1 [20 points total]

  Consider a classical gas of N indistinguishable non-interacting particles with ultrarelativistic energies, i.e. their kinetic energy - momentum relation is given by = pc, with c the speed of light and p the magnitude of the particle's momentum.

  (a) Compute the canonical partition function for this system. [5 points]

  (b) Show that this system obeys the usual ideal gas law, pV = Nk_BT. [5 points]

  (c) Show that the total average energy is, E = 3Nk_BT (and hence with (a), E/V = 3P). [5 points]

  (d) Show that the ratio of specific heats is, C_p/C_V = 4/3. [5 points]

• Problem 2 [20 points total]

  Consider a three dimensional classical ideal gas of atoms of mass m, moving in a potential energy

  

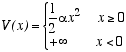
  The infinite potential for x < 0 may be viewed as a rigid wall filling the y-z plane at x=0. The atoms, therefore, are attracted to this wall, but they move freely in the y and z directions. Let T be the temperature and n = N/A be the total number of atoms per unit area of the wall.

  a) calculate the local atomic density n(x) (number of atoms per unit volume) as a function of the distance x from the wall. Note that

  n=

  0

  n(x) dx

  [4 pts]

  b) Show that the ideal gas law (relating pressure, temperature, and density) continues to hold locally everywhere. [4 pts]

  c) Find the pressure that the atoms exert on the wall. How does this pressure vary with temperature? [4 pts]

  d) Calculate the energy and specific heat per unit area of the wall. [4 pts]

  e) Find the chemical potential of the gas. [4 pts]

• Problem 3 [25 points total]

  Consider a classical gas of very weakly interacting molecules of different species. There are N_i molecules of species number i, i = 1, 2, ..., m. The molecules of different species may have different masses and different internal degrees of freedom (such as vibrational or rotational modes), however you may assume that the molecules do not interact with each other. The molecules of a given species are indistiguishable from each other.

  (a) Show that the canonical partition function for the gas has the form

  
  Q = Q⁽¹⁾Q⁽²⁾....Q^(m)      where      Q⁽ⁱ⁾ = [Q₁⁽ⁱ⁾]^N_i/N_i!

  and Q₁⁽ⁱ⁾ is the single particle partition function for molecules of species i. [5 points]

  (b) Using the result in (a), show that the total pressure of the gas is the sum of the pressures that each of the species of molecule would have on its own (total pressure is the sum of the "partial pressures"). Similarly show that the total entropy of the gas is the sum of the entropies that each species would have on its own. [3 points]

  (c) By taking the appropriate derivative of the total Helmholtz free energy of the gas, compute the chemical potential µ_i of species i. Express your answer in terms of Q₁⁽ⁱ⁾. [3 points]

  (d) Assume that the molecules are free (i.e. not in any external potential, except for their confinement to a box of volume V). Show that Q₁⁽ⁱ⁾ can be written as Q₁⁽ⁱ⁾ = Vq₁⁽ⁱ⁾(T) where q₁⁽ⁱ⁾ depends only on temperature T. [3 points]

  (e) Suppose that the species of molecules undergo the chemical reaction

  a₁A₁ + ... + a_jA_j <--> a_j+1A_j+1 + ... + a_mA_m

  where a_i is the number of molecules of species A_i (i = 1,...,j) that combine to create a_k molecules of species A_k (k = j+1,...,m). As discussed in lecture, the equilibrium number of molecules of each species will be determined by the condition

  a₁µ₁ + ... + a_jµ_j = a_j+1µ_j+1 + ... + a_mµ_m

  (make sure you understand where this result comes from!). Use the above, and the results of the previous parts, to show that the equilibrium concentrations of the species are given by

  ([n₁]^a₁ [n₂]^a₂...[n_j]^a_j )/([n_j+1]^a_j+1...[n_m]^a_m ) = K(T)

  where n_i is the concentration of species i, n_i = N_i/V, and K(T) is a function of temperature only. Derive an expression for K(T) in terms of the q₁⁽ⁱ⁾(T). The above result is known as the "law of mass action". [4 points]

  (f) Consider the reaction

  A + B <--> C

  Suppose that an energy E_o is released when A and B combine to form C, i.e. E_o is the binding energy of the molecule C when compared to its separated constituents A and B. Assume that A, B, and C are free point particles (i.e. no internal degrees of freedom are excited). By explicitly evaluating the single particle partition function of the three species, determine the function K(T). Remember, you must properly include the binding energy E_o of molecule C when you compute its partition function. [4 points]

  (g) Suppose that initially there are equal concentrations of A and B, n_A = n_B = n_o, while the concentration of C is initially n_C = 0. Find the resulting equilibrium concentrations of A, B and C, in terms of n_o and the function K(T). [3 points]