|
|

Home
Contact
Info
Course
Info
Calendar
Homework
Lecture
Notes
|
|
|
|
Physics 418: Statistical Mechanics I
Prof. S. Teitel stte@pas.rochester.edu ----- Spring 2005
Problem Set 5
Due Thursday, March 31, in lecture
- Problem 1 [10 points total]
Consider photons of a given energy  = = 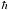  . .
(a) If <n> is the average number of such photons in equilibrium
at temperature T, show that the fluctuation in the number of photons is
<n2> - <n>2 = - (1/ ) (d<n>/d ) (d<n>/d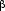 )
where )
where 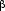 = 1/kBT = 1/kBT
[5 pts]
(b) Using the forumula for the equilibrium value of <n>,
apply the above result to determine the relative fluctuation in the number
of photons
[<n2> - <n>2]/<n>2
Is this large or small? [5 pts]
- Problem 2 [5 points]
The Stefan-Boltzmann law states that a black body at
temperature T radiates power per unit surface area equal to
 T4 where T4 where  is a universal constant
independent of the material properties of the body.
Assuming that the sun and the earth are black bodies,
and that the earth is in thermal equilibrium with the
sun [i.e. energy absorbed = energy emitted] calclate
the temperature of the earth in terms of the temperature
of the sun. Look up the parameters you need in order
to compute a number for this estimate of earth's temperature. is a universal constant
independent of the material properties of the body.
Assuming that the sun and the earth are black bodies,
and that the earth is in thermal equilibrium with the
sun [i.e. energy absorbed = energy emitted] calclate
the temperature of the earth in terms of the temperature
of the sun. Look up the parameters you need in order
to compute a number for this estimate of earth's temperature.
- Problem 3 [25 points]
In the grand canonical ensemble, the probability to have a given state "a"
with total energy Ea and total number of particles Na
is,
Pa =
[e-(Ea-µNa)/kBT]/L
where
L = 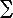 a [e-(Ea-µNa)/kBT]
is the grand canonical partition function. a [e-(Ea-µNa)/kBT]
is the grand canonical partition function.
(a) For a quantum ideal gas, with single particle states i of energy
 i, many particle states are specified by the occupation
numbers {ni} and have energy E = i, many particle states are specified by the occupation
numbers {ni} and have energy E = 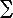 i
[ i
[ ini]. Show that the probability for the state with
occupations {ni} is given by ini]. Show that the probability for the state with
occupations {ni} is given by
P({ni}) = 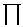 i [pi(ni)] i [pi(ni)]
where pi(ni) is the probability that single particle
state i has occupation ni
pi(ni) =
[e-( i-µ)ni/kBT]/wi i-µ)ni/kBT]/wi
where
wi = 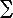 ni [e-( ni [e-( i-µ)ni/kBT] i-µ)ni/kBT]
can be thought of as the partition function
for the single particle state i.
The above factorization says that the number of particles ni
in state i, is independent of the number of particles
nj in state j. [6 points]
(b) Using the above result, show that the Shannon definition of entropy can
be written as
S = -kB 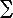 {ni} [P({ni}) ln
P({ni})] = -kB {ni} [P({ni}) ln
P({ni})] = -kB 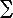 i i
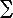 ni [pi(ni) ln
pi(ni)] ni [pi(ni) ln
pi(ni)]
[7 points]
(c) Using the above result, show that the following expressions apply for
the entropies of an ideal gas of bosons and fermions, respectively
| bosons: |
S = kB 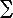 i [(1+<ni>)
ln (1+<ni>) - <ni> ln
<ni>] i [(1+<ni>)
ln (1+<ni>) - <ni> ln
<ni>] |
fermions: |
S = kB 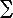 i [-(1-<ni>)
ln (1-<ni>) - <ni> ln
<ni>] i [-(1-<ni>)
ln (1-<ni>) - <ni> ln
<ni>] |
where <ni> = 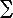 ni
[ni pi(ni)] is the average occupation
number of state i.
[12 points] ni
[ni pi(ni)] is the average occupation
number of state i.
[12 points]
|

