|
|

Home
Contact
Info
Course
Info
Calendar
Homework
Lecture
Notes
|
|
|
|
Physics 418: Statistical Mechanics I
Prof. S. Teitel stte@pas.rochester.edu ----- Spring 2005
Problem Set 7
Due Thursday, April 14, in lecture
- Problem 1 [15 points]
N Fermions A of spin 1/2 are introduced into a large volume V at
temperature T. Two Fermions may combine to create a Boson with
spin 0 via the interaction,
A + A <--> A2
Creation of the molecule A2 costs energy  o > 0.
At equilibrium, the system will contain NF Fermions and
NB Bosons. Provide expressions from which the ratio
NB/NF can be calculated, and perform the
calculation explicitly for T=0. What would this (T=0) ratio be,
if the particles were classical (i.e. quantum statistics can be neglected).
Explain the difference. o > 0.
At equilibrium, the system will contain NF Fermions and
NB Bosons. Provide expressions from which the ratio
NB/NF can be calculated, and perform the
calculation explicitly for T=0. What would this (T=0) ratio be,
if the particles were classical (i.e. quantum statistics can be neglected).
Explain the difference.
- Problem 2 [15 points]
A linear molecule of N identical atoms has a vibrational spectrum given by the angular frequencies,
 m= m= osin(m osin(m /2N),
for m = 1,2, ..., N-1 (i.e. these are the frequencies of the normal modes of vibration). /2N),
for m = 1,2, ..., N-1 (i.e. these are the frequencies of the normal modes of vibration).
a) Show, by explicit calculation, that the vibrational contribution to the specific heat of this molecule at very high temperature, T-> , is , is
C = (N-1)kB
b) Show that for lower temperatures, such that 1/N << kBT/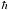  o << 1, o << 1,
C ~ T
c) How does C vary with temperature at very low temperatures, such that
kBT/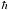  o << 1/N? o << 1/N?
- Problem 3 [25 points]
Consider a gas with hard core inter-particle interactions, i.e.
| u(r) | = | infinity
0 | for r<ro
for r>ro |
(a) Compute the 2nd and 3rd virial coefficients, B2 and B3 for d=1 dimension (hard rods).
(b) Do the same for d=2 dimensions (hard disks).
(c) Compute the isothermal compressibility,  T, in terms of the virial expansion to 2nd order, i.e. through B2 and B3. T, in terms of the virial expansion to 2nd order, i.e. through B2 and B3.
(d) Compute the specific heat at constant pressure, Cp, in terms of the virial expansion to 2nd order, i.e. through B2 and B3. (Hint: to compute Cp you might wish to use the formula that relates it to CV,  T, and the coefficient of thermal expansion T, and the coefficient of thermal expansion  .) .)
(e) Using your results in parts (a) and (b), and using Pathria Eqs. (9.3.15) and (9.3.20) to get B2 and B3 for hard spheres in d=3 dimensions, make a table showing how  T and Cp-CV vary with dimension d for hard core interactions. Comment on any trends you see. T and Cp-CV vary with dimension d for hard core interactions. Comment on any trends you see.
|

