- Problem 1 [10 points total]
Prove the following relationship between the specific heat at constant pressure, Cp, and the coefficient of thermal expansion α.
(∂Cp/∂p)T = −TV[α2 + (∂α/∂T)p]
- Problem 2 [15 points total]
In a particular engine a gas is compressed in the initial stroke of the piston. Measurements of the instantaneous temperature, carried out during the compression, reveal that the temperature increases according to the relation:
T = (V/Vo)ηTo
where To and Vo are the initial temperature and volume and η is a constant. The gas is compressed to the volume V1 (where V1 < Vo). Assume that the gas is a monatomic ideal gas of N atoms, and assume the process is quasi-static (i.e. the system is always instantaneously in equilibrium).
a) Calculate the mechanical work done on the gas. [5 points]
b) Calculate the change in the total energy of the gas. [5 points]
c) Calculate the heat transfer Q to the gas. For what value of η is Q = 0? Show that this corresponds to the case of adiabatic compression (see Problem 1f). [5 points]
[Hint: you may use the facts you know about an ideal gas, i.e. pV = NkBT, and E = (3/2)NkBT.]
- Problem 3 [15 points total]
A thermodynamic engine can be thought of as a cyclic process by which heat (TdS) pumped from a "hot" reservoir into a system (the engine) is converted into mechanical work (pdV) done by the engine. The most famous such example is the Carnot cycle. Another such cycle is the Otto cycle, schematically shown in the diagram below as a directed path in the volume-entropy plane. The Otto cycle is a rough approximation to the operation of a gasoline engine.
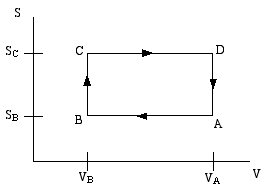
The gas is compessed adiabatically (constant entropy) in the step A to B. Then it is heated isochorically (constant volume) in the step B to C (this step corresponds to the combustion of the gas in the gas engine). The gas is then expanded adiabatically in step C to D (this is the power stroke). Finally the gas is cooled isochorically to bring it back to its initial state; this is step D to A.
Step B to C extracts heat QBC from the "hot" reservoir to heat the gas, while step D to A returns heat QDA = − QAD to the "cold" reservoir (usually the ambient atmosphere). The difference is the work done by the engine.
If the engine efficiency is defined as ratio of the net heat converted to work, divided by the heat withdran from the hot reservoir
ε = (QBC − QAD)/QBC
then assuming the gas is an ideal gas, show that the efficiency of the Otto cycle is given by,
ε = 1 − (VB/VA)(Cp − CV)/CV
(Hint: for this problem, read the supplemental notes to lecture 6.)