Home

Research

CV

Publications

Conference
Participation

Seminars Given

Group Members

Teaching

Misc

Condensed Matter Group

UR PAS

The Jamming Transition in Granular Materials

In granular materials, in which thermal fluctuations are believed to be negligible, a jamming transition has been proposed: upon increasing the volume density (or "packing fraction") of particles ρ above a critical ρ_c, the sudden appearance of a finite shear stiffness signals a transition between a flowing liquid and a rigid but disordered solid state.

Similar behavior has been observed in other systems. In foams, comprised of polydisperse densely packed gas bubbles embedded in a dilute liquid host, decreasing an applied shear stress below a critical yield stress causes the foam to transform from a flowing liquid to an elastic solid. In glassy forming liquids, decreasing the temperature causes an apparent divergence in viscosity, resulting in a transformation from a liquid to a frozen glassy state, referred to as the "structural glass transition".

It was recently proposed by Liu and Nagel and co-workers that these various phenomena, all involving a transformation from a flowing liquid state to a rigid but disordered state, might represent different manifestations of a unified jamming phase diagram in a three dimensional phase space consisting of temperature T, density ρ and applied shear stress σ. A surface in this three dimensional parameter space would then separate jammed from flowing states. The intersection of this surface with the ρ-σ plane at T=0 describes the athermal jamming of shear driven foams and granular material. The intersection of the surface with the ρ-T plane at σ=0 would descibe the thermally driven structural glass transition. The pure density driven jamming at T=0, σ=0, was proposed as a special 2nd order critical point, dubbed "point J". The hope is that by studying the simpler jamming of granular materials, one will thus also be able to learn something about the structural glass transition, which is generally regarded as one of the greatest remaining problems of condensed matter physics. Including the applied shear stress σ in the phase diagram also extends the desription of behavior in such systems from purely equilibrium situations (σ=0) to non-equilibrium driven steady states (σ>0), thus making it an interesting system in which to study critical phenomena far from equilibrium.

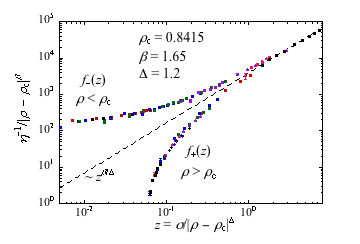
To investigate these issues we have carried out numerical simulations of a two dimensional, shear driven, model granular system of bidisperse soft core disks. Varying the areal density of disks, ρ, and the driving shear stress, σ, at zero temperature, T=0, we compute the shear viscosity, η, of the resulting shear flow. If point J, at ρ=ρ_c, σ=0, does indeed behave like a 2nd order critical point, then behavior nearby at finite σ and ρ close to ρ_c is governed by the critical singularity at point J. In particular, we expect that near point J the viscosity η(ρ,σ), as a function of the two variables ρ and σ, should collapse to a universal scaling curve depending on only a single scaling variable, σ/|ρ-ρ_c|^Δ, where Δ is the crossover scaling exponent characterizing the effects of turning on a finite shear stress σ.

click on plot to enlarge

We indeed find an excellent agreement between our numerical results and this expectation, with our data for the inverse viscosity, η^-1, collapsing to the scaling form,

η^-1(ρ, σ) = |ρ-ρ_c|^βf(σ/|ρ-ρ_c|^Δ),