Home

Research

CV

Publications

Conference
Participation

Seminars Given

Group Members

Teaching

Misc

Condensed Matter Group

UR PAS

Lattice Gas Models for Non-Equilibrium Steady States: Application to a Driven Two Dimensional Vortex Lattice

When a time independent force, with non zero spatial average, is applied to a system of interacting particles, a time independent non-equilibrium state with a finite current will in general result. While the theory of phase transitions between equilibrium states is well developed, the phase transitions between such driven non-equilibrium steady states are less well understood.

Numerical studies of such problems often involve the simulation of continuous time stochastic equations of motion for particles moving in a spatial continuum ("molecular dynamics"). In contrast, in the theory of equilibrium transitions, significant progress was achieved by the introduction of lattice models, in which degrees of freedom are restricted to a discrete lattice of spatial sites. In addition to the analytical simplifications introducted, the great reduction of phase space in such lattice models means that numerical simulations can often be more efficient and accurate.

We are seeking to develop similar lattice models for non-equilibrium states, in which particles will be restricted to discrete hops between spatially discrete lattice sites.

structure function of a moving smectic

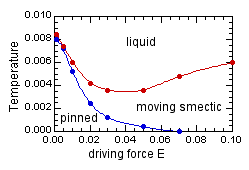
As a simple model system, we have considered the case of the driven 2D lattice Coulomb gas as a model for driven vortices in a 2D Josephson junction array or thin superconducting film with a periodic pinning potential. We first considered a commonly used "drift diffusion" algorithm which seeks to extend the common equilibrium Metropolis Monte Carlo method to non-equilibrium steady states. However we have found this algorithm to give unphysical results: even at vanishingly low temperatures, the ordered vortex lattice melts into a liquid, once it unpins and starts to move. We have therefore developed a new dynamic algorithm based on sampling the hopping rates for all possible moves at any given time. With this new algorithm we find, above a critical driving force in the limit of vanishing temperature, the physically expected moving ordered vortex lattice. However, at finite temperature, this moving vortex lattice becomes a moving vortex smectic phase; vortices move in well defined periodic channels parallel to the driving force, however relative motion within different channels has only a short range correlation. This work was carried out in collaboration with graduate students Violeta Gotcheva and Yanting Wang, and undergraduate student Albert Torr-Jong Wang. Details may be found in Phys. Rev. Lett. 92, 247005 (2004) and in Phys. Rev. B 72, 064505 (2005).