Our target exoplanet is commonly known as HAT-P-53 b.

Summary of our measurements:

Planetary radius = 1.4 ą 0.1 Jupiter radii
Planetary orbital period = 1.96190 ą 0.00007 days.
Planetary orbital radius = 0.031565 ą 0.000001 AU
Planetary temperature = 2175 K
Hypothetical moon temperature = 1722 K (fast rotator) >> 373 K

The planet is a Hot Jupiter. Neither the planet, nor any moons it may have, are habitable.

The following is about how we obtain these measurements and their immediate consequences, from our data. It is not a model term paper; you need not have presented such detail in your discussion of how the light curves lead to the planetary parameters.

First, work out the depth of the transit, from all the light curves. I averaged the points for dates 0.10-0.14 days (light curve 1), 6:00-6:03 days (2), and 60.00-60.95 days (3) for the transit and 0.16-0.20 days, 6.045-6.100 days, and 60.97-61.10 days respectively for the baseline, and got

Transit signal = 0.987 ą 0.002
Baseline signal = 1.001 ą 0.001

(You didn't have to report statistics and propagated uncertainties in your term paper, but I will do so here.)

This makes the transit 1.3% ą 0.2% deep. Using formula #3 on our Useful equations page (see also the lecture notes for 21 September 2021, page 5), and the 11.8 Jupiter-radii radius of the star as listed here under The Host Star, we get

Planet radius = 1.4 ą 0.1 Jupiter radii

for the transiting planet. Rocky planets don't come in this size, as we learned on 21 September 2021. It's a gas giant -- a Jupiter -- and thus we already know that it is not habitable.

Next, work out the times of egress for the three light curves. It's best to sketch smooth curves through the data and find the point in the egress that lies halfway between the transit signal and the baseline signal. Like this:


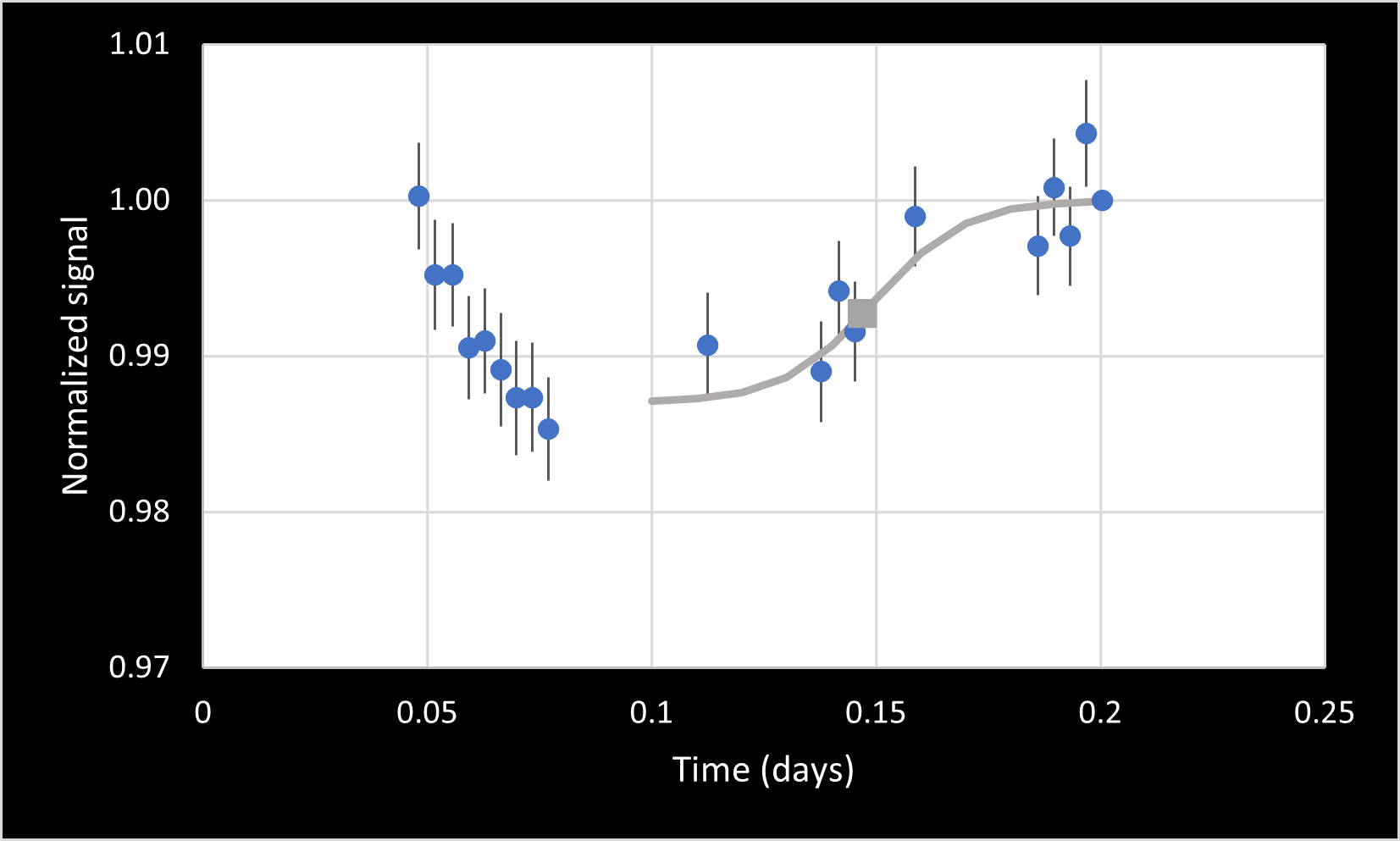
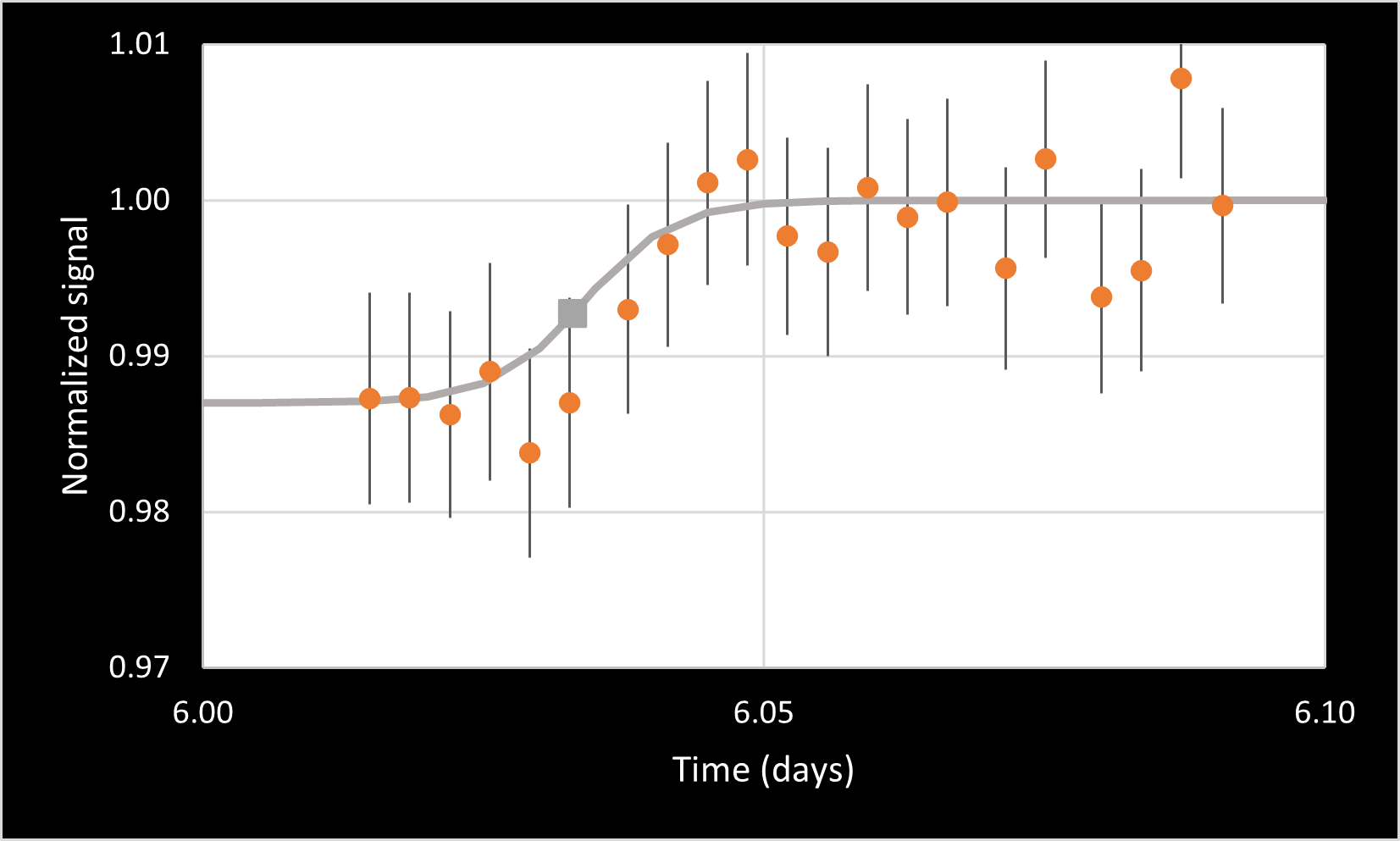
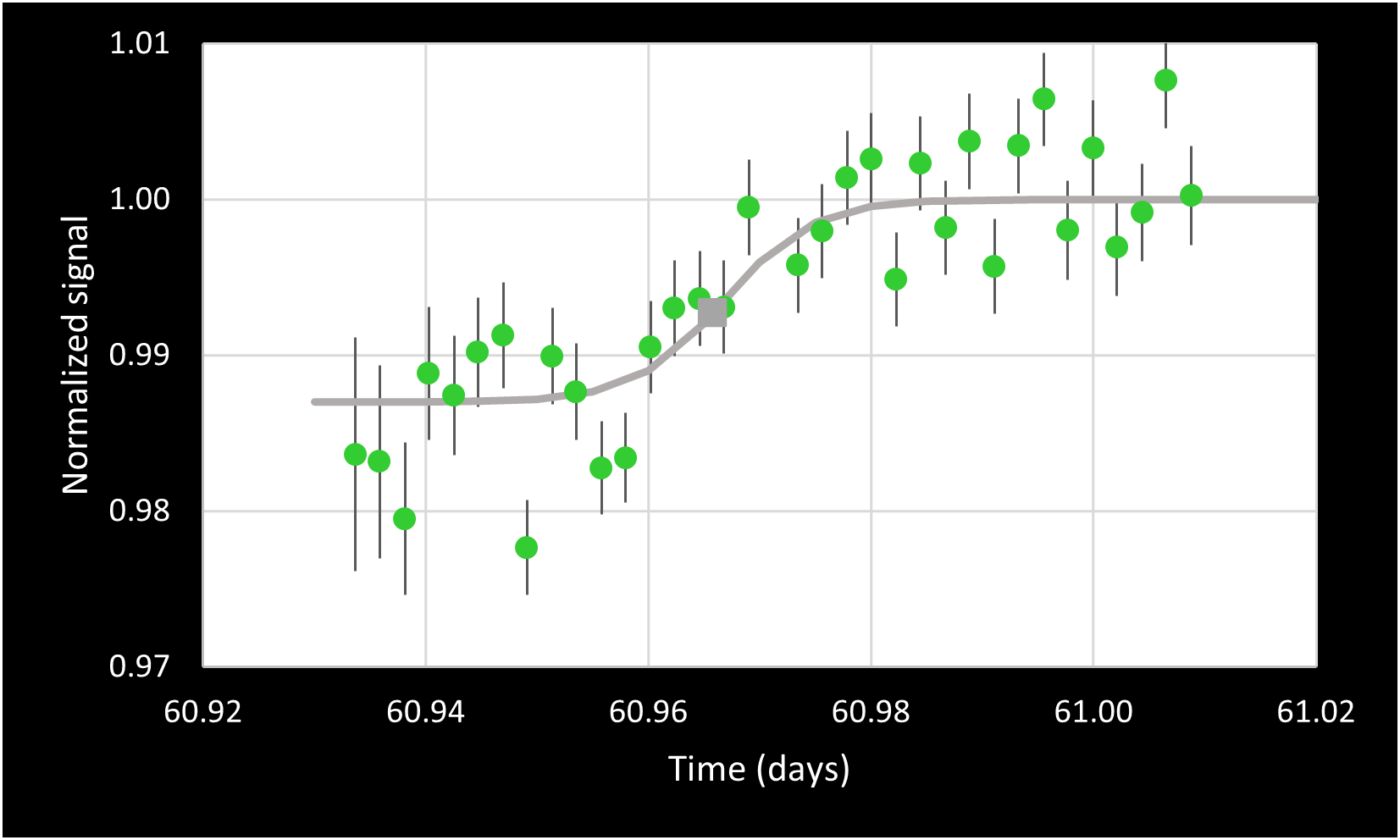
(These are fitted curves, but freehand sketches would be just as good.) Thus we get the times of egress, measured the same way on each light curve, and indicated above with square markers: Egress 1 = 0.147 ą 0.002 days Egress 2 = 6.033 ą 0.001 days Egress 3 = 60.966 ą 0.001 days The intervals between the egresses are Interval 1-2 = 5.866 ą 0.002 days Interval 2-3 = 54.933 ą 0.001 days Interval 1-3 = 60.819 ą 0.002 days Divide long intervals by short ones: this gives (Interval 1-3)/(Interval 1-2) = 10, with a remainder of 1.962 days (Interval 2-3)/(Interval 1-2) = 9, also with a remainder of 1.962 days Thus the orbital period must be about 1.962 days or shorter -- half of this, or a quarter, etc. Taking the remainder to be the first approximation to the orbital period, we can work out the number of orbits of HAT-P-53 b during the the intervals between transit observations: Interval 1-2 = 5.866/1.962 orbits = 3.000 orbits (compare to the Hint) Interval 2-3 = 54.933/1.962 orbits = 28.000 orbits Interval 1-3 = 60.819/1.962 orbits = 31.000 orbits Of course they're not 3.000, 28.000, and 31.000 orbits: there is an exact, integer number of orbits between any two egresses. So these intervals are exactly 3, 28, and 31 orbits long. This gives us our most accurate measurement of the orbital period: take Interval 1-3 and its uncertainty, and divide both by 31: Orbital period = 1.96190 ą 0.00007 days. Why are we calling this the orbital period now, rather than "the longest the orbital period can be"? Because if it were shorter than this, it would have to be shorter by a factor of 1/2, or 1/3, or 1/4, etc. to lead also to the transits we observed. Very short periods can be ruled out, because we would have seen multiple transits on the same night, and did not. The next shorter possibility is 1/2 of 1.96190 days, or 0.981 days = 23.5 hours. On 13 December, egress was observed at about 6:20 PM. If the orbital period were 23.5 hours or any of the allowed shorter ones, we would have seen another transit on 12 December, at 6:50 PM. And we did not, as shown in Light Curve 2.9. So 1.96190 days it is, unambiguously. Next, we use the orbital period to calculate the orbital radius and temperature of the planet and any moons it may have. From Formula #4 on our Useful equations page, or the lecture notes for 21 September 2021, we get Orbital radius = 0.031565 ą 0.000001 AU That's very close to the star: only 5.6 stellar radii. We can therefore assume the planet is tidally locked, and slowly rotating. From close up -- say, from a vantage point 1 AU away from the star -- our target exoplanet and its star would look something like the image at right (courtesy of Tim Pyle at Caltech). Now let's assume that, since the planet is Jupiter-size, it has a Jupiter-like albedo -- 0.44, according to our Physical constants page. Then the temperature of the sunlit face, according to Formula #5 on our Useful equations page or page 16 of the 23 September 2021 lecture notes, is Temperature = 2175 K. Thus our planet is a Hot Jupiter. (See the lecture notes for 21 September 2021, page 7.) Next, let's also assume that it may have rocky moons which have Mercury-like albedo -- 0.12, also according to our Physical constants page. Like all moons of giant planets the rotation of these hypothetical moons would be tidally locked to their orbits around the planet, and lie at close to the same distance away from the star as the planet. Being tidally locked to their orbit around the planet is not the same as being tidally locked in orbit around the star: such moons would almost certainly not have permanently sunlit and dark sides. But it doesn't really make much difference: according to Formulas #2 (rapid rotator) and #5 (slow rotator) on our Useful equations page, the moons would all have Temperature = 2435 K (slow rotator) or 1722 K (fast rotator) >> 373 K. The fast rotator possibility is a lot more likely. Either way, though, the hypothetical moons would not be habitable. Far from it: they would be flaming lumps of magma with no water or organics on the surface. We were not the first to observe this exoplanet, HAT-P-53 b; how did we do, compared to other observations, usually at better observing sites? Pretty well, considering how ratty our data look, and how much we had to give up to the clouds. Here are the results listed for HAT-P-53 b in the NASA Exoplanet Archive, compared to ours:
Quantity Planetary radius, Jupiters Planetary orbital period, days Planetary temperature, K Planetary type	Us 1.4 ą 0.1 1.96190 ą 0.00007 2175 Hot Jupiter	Them 1.318 ą 0.091 1.9616241 ą 0.0000039 1778 ą 48 Hot Jupiter