Motivation
If stars are born out of the turbulent condensations of the interstellar medium, what determines the final mass of the star? Is it the mass and structure of the condensation? The interplay between various physical processes in the gas? A combination of both?
The answers lie with understanding how the various physical processes in the prestellar environment (magnetic fields, mechanical and radiative feedback, gravity, etc.) couple to the natal gas. Indeed, state of the art simulations suggest that each of these processes is significant, yet a clear theoretical framework for how these processes couple to the gas is lacking. Developing such a framework would significantly advance the following key open questions in the field:
- What sets the 'coupling efficiency' in the prestellar environment, and how does this give rise to the initial mass function (including both the stellar and substellar populations?)
- Do filaments play a passive or active role in shaping the mass distributions of stars, and what is this role?
In what follows, I will highlight key results from my research and outline my future directions.
Molecular cloud dynamics
Turbulent motions in molecular clouds generate filaments, and inside of these filaments lie protostellar cores, the seeds of star formation:
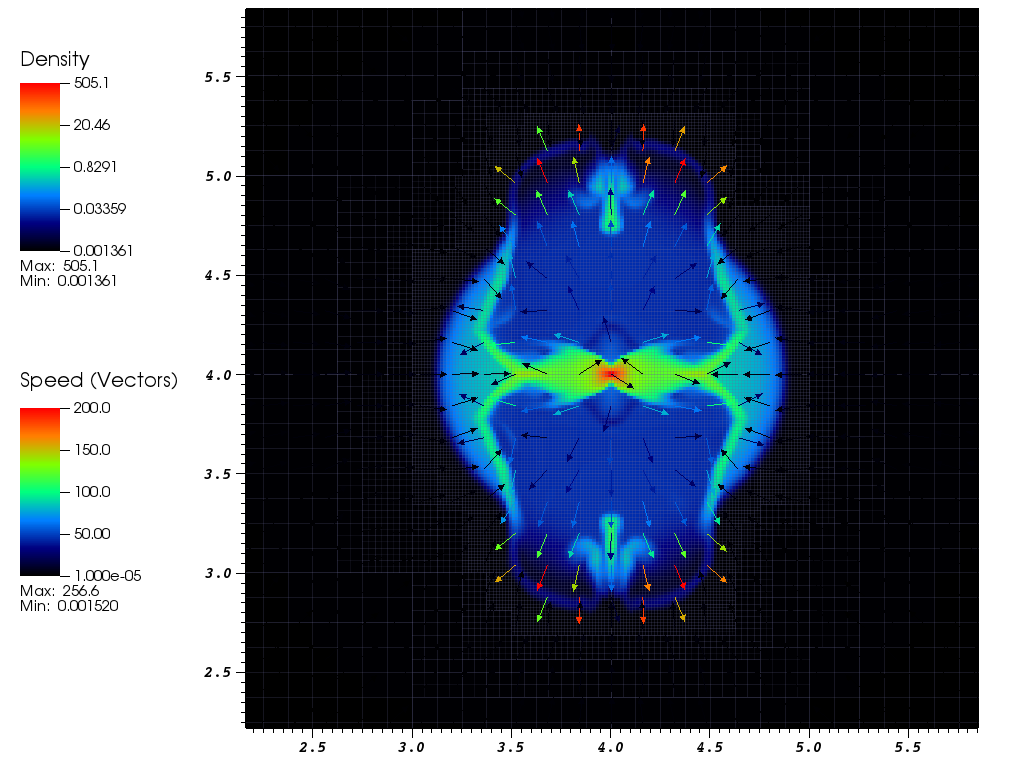
How these filaments are oriented with respect to the background magnetic field is currently of huge interest to the star formation community. In the plot above, the local magnetic field direction is given by the black vectors.
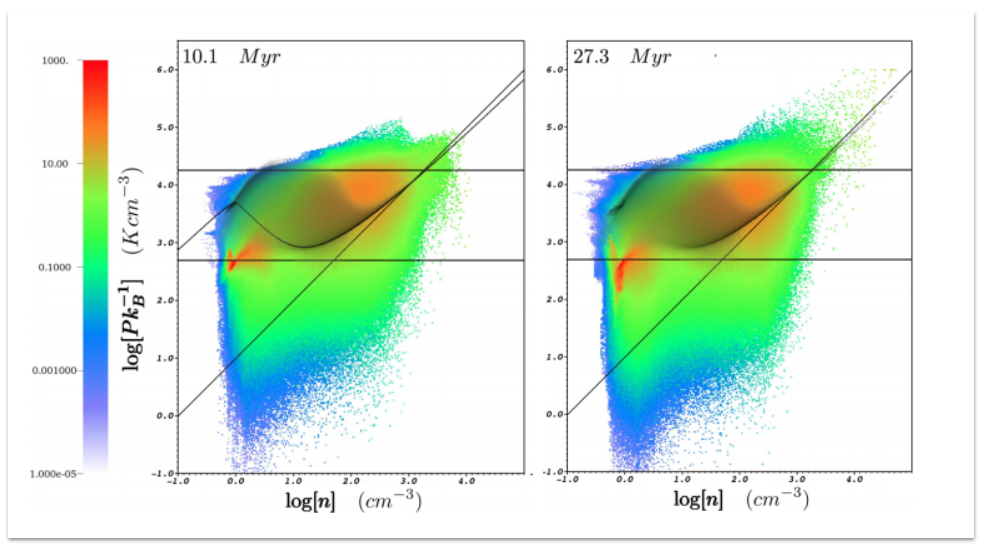
The star formation inside of cores is greatly impeded when magnetic fields are present. The stronger the field becomes, the more it supports the gas against gravitational collapse. The following 2D histogram shows that the magnetic pressure (y-axis, color plot) is highest in the densest gas. This indicates that as gas collapses in molecular clouds, the magnetic pressure increases as well, and this is due to field line compression. Note, the color of the distribution gives the amount of mass at the given pressure, density coordinate.
Shear in molecular clouds further amplifies magnetic fields on the core scale. As shown by the following power spectra, the magnetic energy (dashed lines) is amplified when more shear is present in the environment:
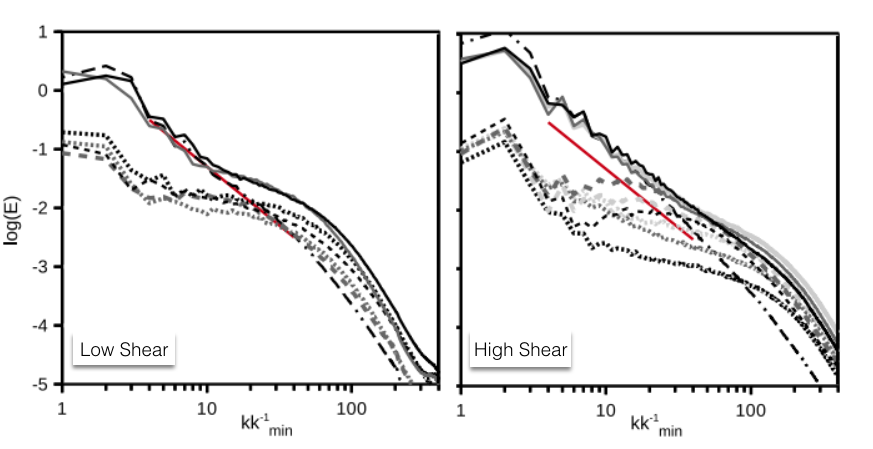
As the shear dissipates with time (going from black to light gray), the magnetic energy declines.
Conclusion: Magnetic field amplification occurs in highly dynamic environments and slows star formation. Mechanisms must exist that remove the excess magnetic energy so that star formation can take place.
Magnetized filament formation
Simulations of the turbulent interstellar medium (ISM) show that regions of converging flows naturally arise (cf. early work by Vazquez-Semadeni et al. 1995). Dense filaments form at the junction of these flows, and thus, converging flows represent one mechanism for building filamentary structure in the ISM.
Observations of the interstellar magnetic field indicate that the field is preferentially aligned normal to dense filaments. We have shown that the reorientation of oblique, magnetized shocks is one way to produce this perpendicular configuration. In this model, the interaction between post-shock gas and the magnetic field forces the filament to become normal to the background magnetic field.
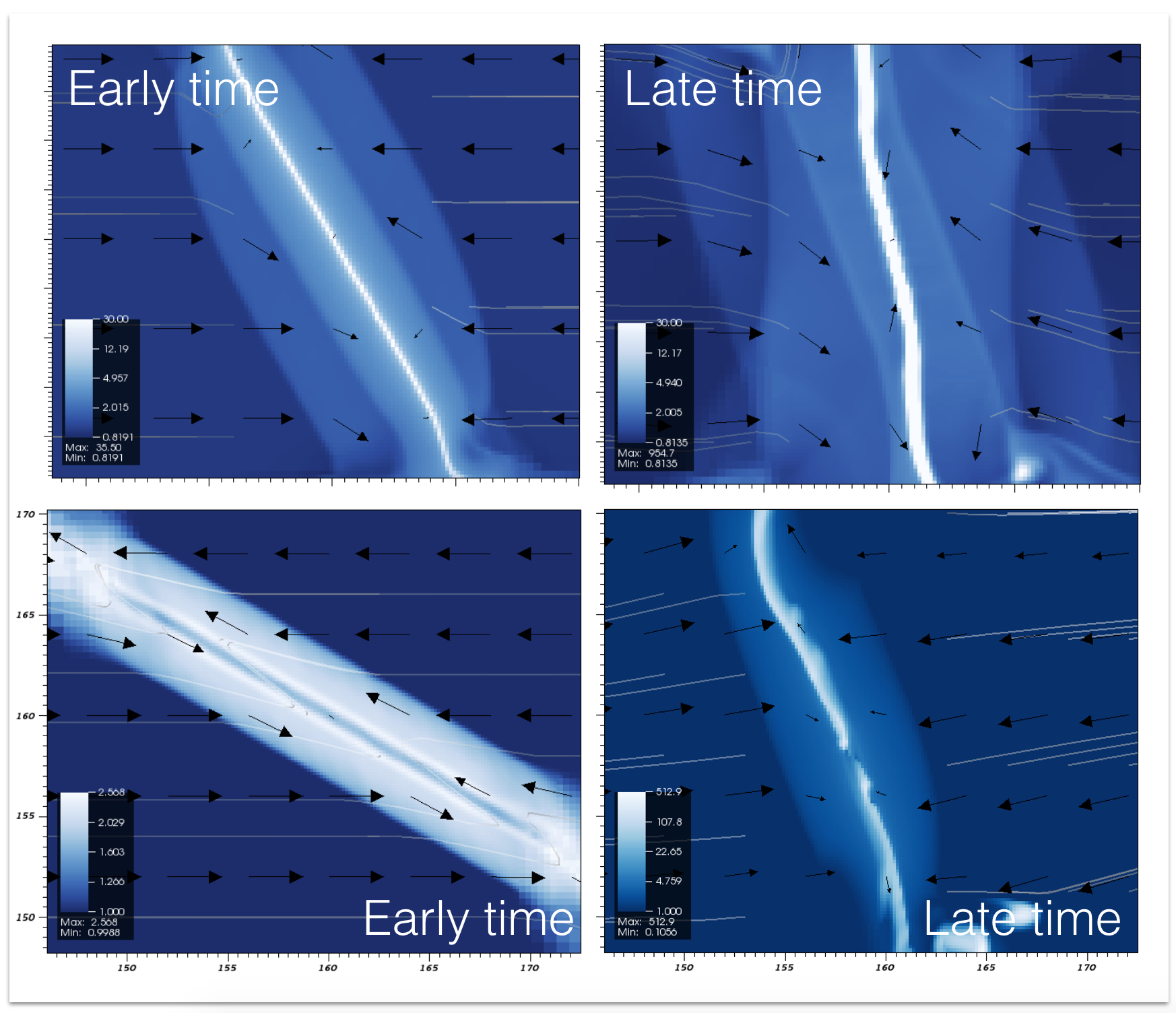
Even when the filament and the field start out highly oblique, the filament reorients normal to the magnetic field. A time sequence illustrating this process is shown below for two different obliquities, where the color bar gives density and background magnetic field lines (light gray) and velocity vectors (black) are overlaid:
Compression-induced protostellar collapse
If the earliest stages of star formation begin with a quasistatic, spherical clump of gas, how does this clump interact gravitationally with its environment? To answer this question, we embedded a marginally stable, hydrostatic sphere (aka a 'Bonnor-Ebert' sphere) into a highly idealized environment (namely, a uniform, static background) and allowed the simulation to evolve dynamically. We found that the sphere gravitationally accelerates the ambient gas. Ram pressure perturbations of the infalling ambient gas at the surface of the sphere drive compression waves into the sphere's interior. The amplitude of these waves are a function of the weight of the environment, and can be strong enough to trigger collapse of the sphere itself.
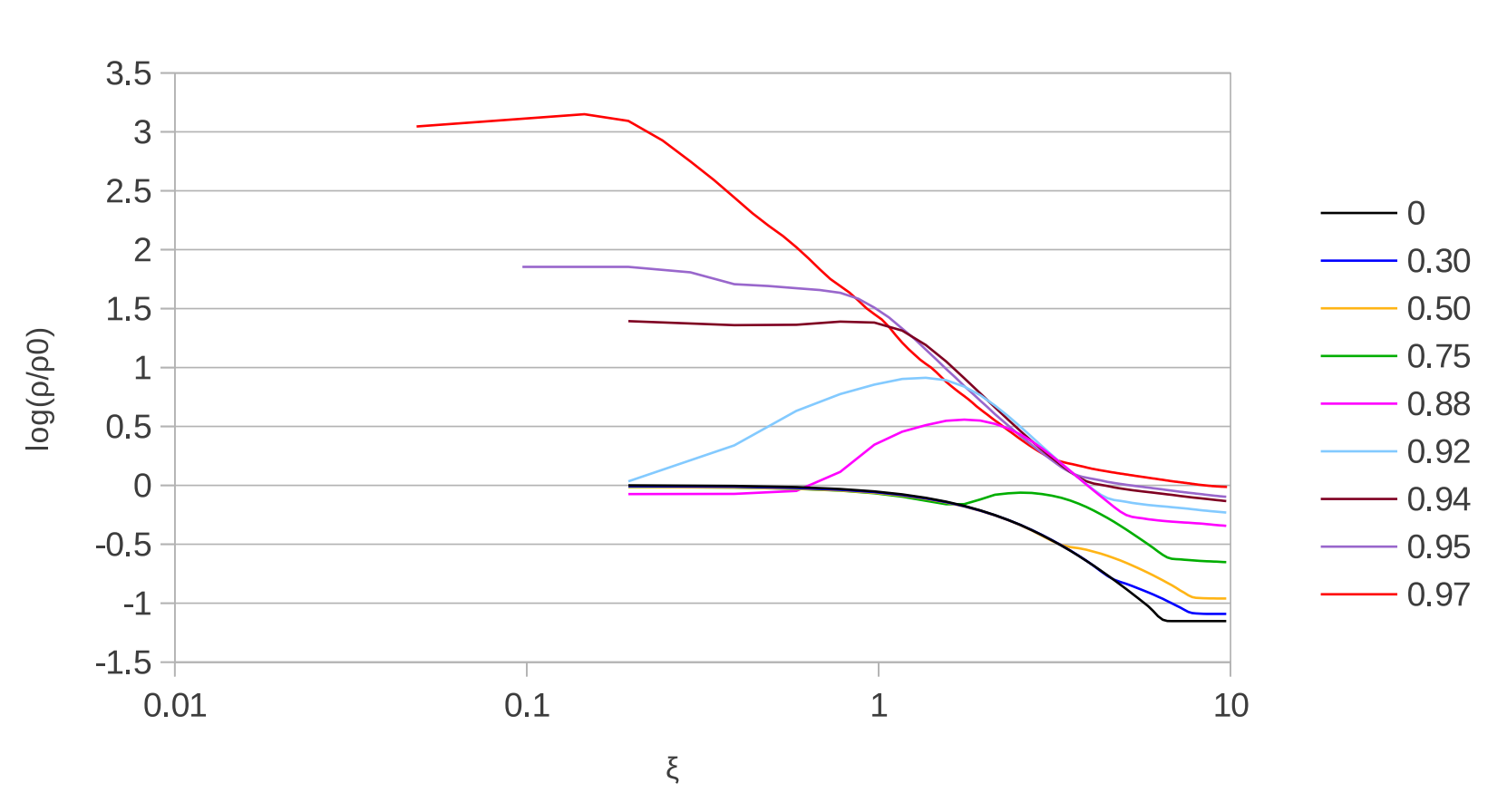
Interestingly, even when collapse is initiated by compression waves, the well-known collapse profiles of Bonnor-Ebert spheres eventually emerge. To illustrate this, here are the radial density (ρ) profiles of the sphere + environment (as a function of radius, ξ), over time, in the case of compression-induced collapse:
compared to the characteristic collapse density profiles of an unstable sphere itself:
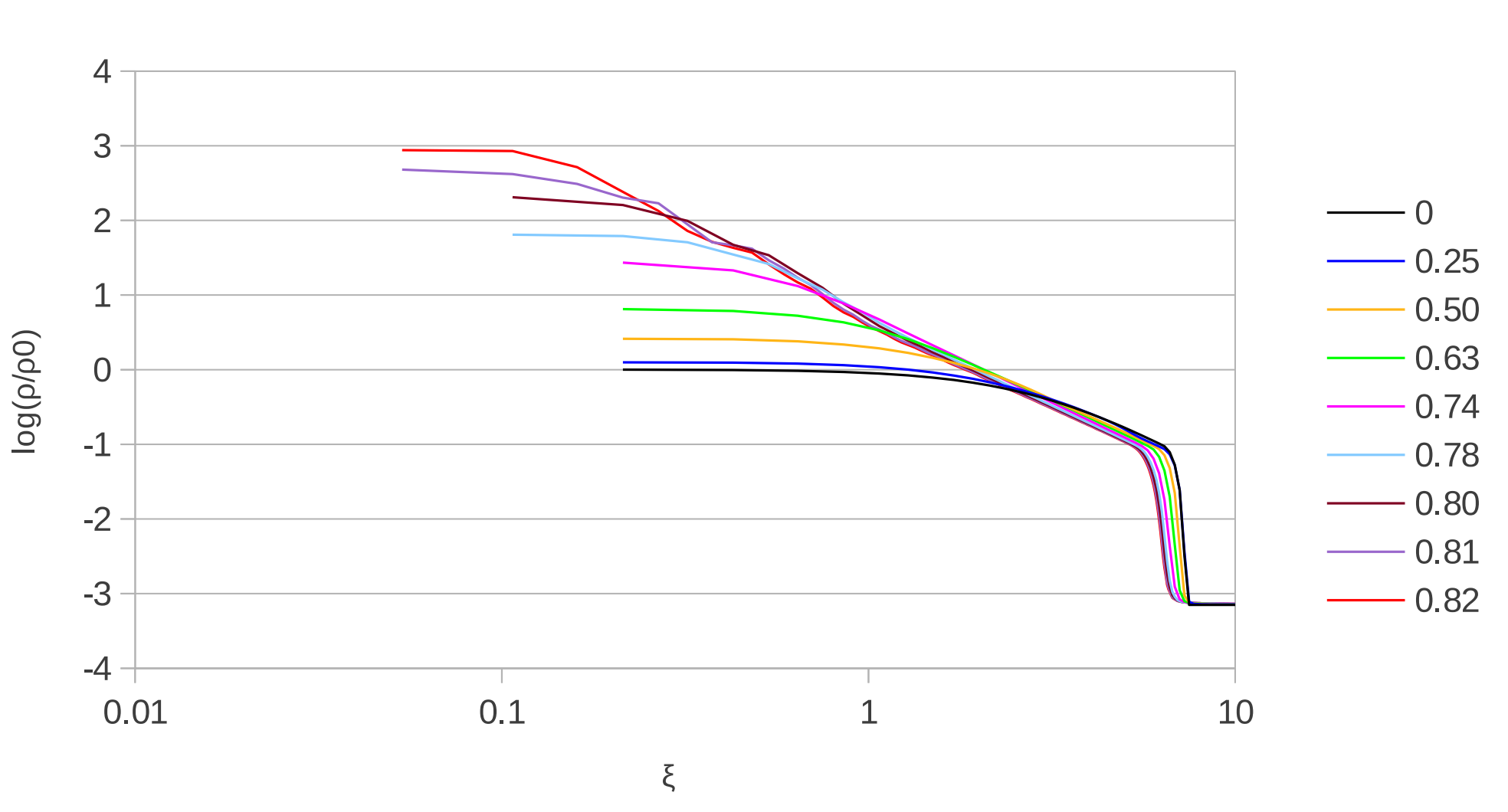
Notice in the top plot, at early times, compression waves enter the sphere from the ambient medium. This triggers collapse, as evident by the increasing density of the sphere. At late times, the profile becomes flat-topped in the inner regions, flanked by a roughly ξ-2 tail. This is the classic shape of a collapsing Bonnor-Ebert sphere, as shown in the bottom plot. This indicates the collapse profiles of Bonnor-Ebert spheres are robust, as they are recovered even in the case of compression wave induced collapse.
Feedback
Now that I have worked on star formation from cloud scales down to protostellar scales, I would like to come full circle by adding feedback. In particular, I would like to extract a cloud from my molecular cloud simulations and zoom-in to a collapsing core within the cloud. From there, I would increase the resolution of the collapsing core and follow its evolution down to AU scales. Once a protostar forms, I will then be able to follow the interaction between the feedback and the environment. Taken together, I am now in the position to study the coupling between various feedback processes and the interstellar environment, self-consistently.
The feedback routines I will be using include a two component outflow (wide angle slow wind + fast collimated jet) following Federrath at al. 2014. I have also built radiative feedback into the sink particle routines of AstroBEAR, which tracks and emits the accretion luminosity of the growing protostar using radiative transfer in the flux-limited diffusion approximation (following Krumholz et al. 2007).
The following image shows preliminary data for a collapsing core with feedback. This is a rotating, supercritical Bonnor-Ebert sphere that has collapsed to form an accretion disk, central protostar, and outflow. As can be seen from this image, the outflow has just broken free of the core, and is beginning to propagate out into the ambient medium: