For the purpose we have in mind, namely the singularity theorem, we need
to apply the above ideas to null geodesics. We began with timelike
curve because one needs to compute in order to have a good
feeling of what is happening! Also the computation are easier
in the timelike case.
The formula look the same than in the timelike case. The main difference is that we now have a null tangent vector so we use a pseudo-orthonormal base.
Again the convergence of this geodesic is at a finite affine parameter.
The idea of converging light rays is not disturbing for us,
the picture 
is normal in the context of an optical lense.
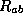
Figure: Converging light ray in optics
But imagine for one moment what result this would have if it happened to the spacetime .
There is a problem with causality! Indeed one can see the geodesic as the minimized distance between two points. Then, with the conjugate points, one loose the idea of uniqueness of the solution! There are two minimizing curve!
To give more meaning to that equation let us show the computation in the Schwarzschild case. The metric is given by
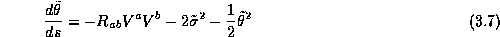
It is the first exact solution of the
Einstein equation (see appendix page ). An important feature of that solution is the horizon r=2m.
Let us take the radial outward null geodesic in the Schwarzschild case.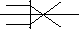 
. We have, from the geodesic equation, 
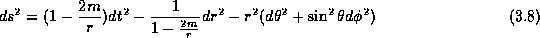. And as 
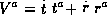we can find the 
.
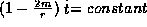By using the Christoffel symbol (see appendix page for a definition and appendix page for GR-Tensor which can compute it) one can find
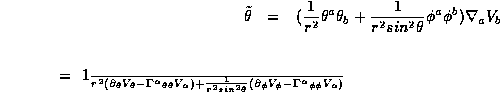
Then one can see that on the horizon r=2m,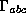 
vanishes and behind the horizon, r<2m, we have 
. This means that everything that go through the horizon converge. In fact we will show later that behind the horizon everything hit the singularity.
This computation was also done in the case of the Robertson and Walker solution (cosmology) in the appendix page .
