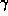
The de Sitter metric is:
The penrose diagram of this spacetime is given in figure 
. One can see from it that this space is not asymptotically flat. An important feature of that spacetime is the fact that it has a spacelike null infinity. This leads to some apparent horizon.
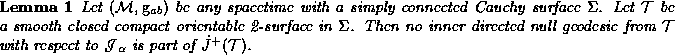
Figure: Penrose diagram of de Sitter spacetime
It is the model of an exponentially growing universe of constant curvature R>0.
We calculate the volume expansion to be:
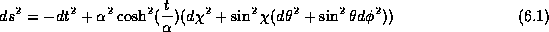
It is always positive. There is no convergence of geodesics in that spacetime
.
In the de Sitter spacetime (for the slicing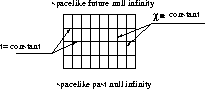 
) we have 
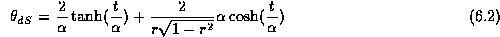which is closed and connected. These hypothesis on 
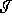are the one needed for the demonstration of the lemma 2 of the Topological Censorship
theorem. The generalization of the Topological Censorship
is then possible.
