The first lemma (page ![]() ) state that:
) state that:
Let 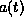 be any spacetime with a simply connected Cauchy surface
be any spacetime with a simply connected Cauchy surface
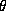 . Let
. Let 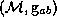 be a smooth closed compact orientable
2-surface in
be a smooth closed compact orientable
2-surface in 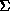 . Then no inner directed null geodesic from
. Then no inner directed null geodesic from 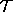 with respect to
with respect to  is part of
is part of 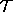 .
.
Proof. Let t be a time function for which 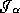 is a surface of constant
t, and let
is a surface of constant
t, and let 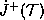 be the orbit of
be the orbit of  under diffeomorphisms
generated by
under diffeomorphisms
generated by 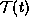 . As
. As 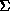 is simply connected, the
timelike surface
is simply connected, the
timelike surface 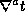 separates the spacetime into disjoint
parts, interior and exterior to the surface. Each infinite affine parameter inner-directed null
geodesic
separates the spacetime into disjoint
parts, interior and exterior to the surface. Each infinite affine parameter inner-directed null
geodesic 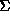 from
from 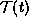 must first
intersect
must first
intersect 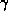 for t > 0 at a point p. But p is in the
timelike future of
for t > 0 at a point p. But p is in the
timelike future of 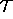 :
: 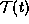 . Thus p cannot
lie on
. Thus p cannot
lie on 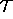 , and
, and 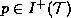 cannot be a generator of
cannot be a generator of
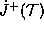 .
.
And now the proof of the lemma ![]() page
page ![]() . first let us recall it.
. first let us recall it.
Let M be a spacetime with a simply connected Cauchy surface 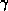 . Let the metric be de Sitter outside of a compact set S. Let S be such that
. Let the metric be de Sitter outside of a compact set S. Let S be such that 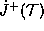 is not empty. Then no trapped surface
is not empty. Then no trapped surface 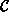 in
in 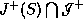 intersect
intersect 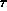 .
.
Proof. Because we take the outside metric to be de Sitter we have 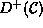 which is inside
which is inside 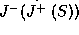 .
This means that
.
This means that 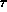 .
We do this proof by contradiction. We assume that
.
We do this proof by contradiction. We assume that 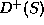 is not empty.
Let
is not empty.
Let 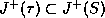 . There exists a curve
. There exists a curve 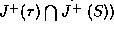 from
from 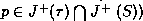 to p.
Like
to p.
Like 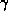 there exists through p a null geodesics
there exists through p a null geodesics 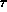 with an infinite length.
with an infinite length.
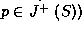 must be a null geodesics in
must be a null geodesics in  , because if it is not then one can find a shorter curve and therefore p is not in
, because if it is not then one can find a shorter curve and therefore p is not in 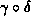 . And
. And 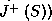 has an infinite affine parameter.
This means that we have a null geodesic with an infinite lenght from a trapped surface.
This is the contradiction because, as
has an infinite affine parameter.
This means that we have a null geodesic with an infinite lenght from a trapped surface.
This is the contradiction because, as 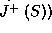 is trapped surface, there must be a conjugate point within a finite affine parameter. Therefore
is trapped surface, there must be a conjugate point within a finite affine parameter. Therefore 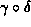 cannot run to infinity.
Then
cannot run to infinity.
Then 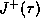 is empty.
is empty.