First let us recall the theorem ![]() :
:
Let M be a globally hyperbolic spacetime which satisfies the averaged null energy condition (ANEC) . Let the metric be de Sitter outside of a compact set S. Let S be such that  is not empty. Then any topological structure in S surrounded by an inner trapped surface cannot be probed.
is not empty. Then any topological structure in S surrounded by an inner trapped surface cannot be probed.
Proof of Theorem 1. Consider the universal covering space
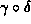 and the corresponding
spacetime
and the corresponding
spacetime 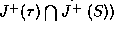 , with
, with 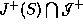 the pullback
of
the pullback
of 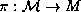 to
to 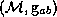 by
by 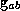 . By construction
. By construction 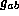 is
simply connected, and any point in M has a simply connected
neighborhood A whose inverse image
is
simply connected, and any point in M has a simply connected
neighborhood A whose inverse image 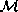 is the disjoint
union of open simply connected sets in
is the disjoint
union of open simply connected sets in  . Each of these
copies of A in
. Each of these
copies of A in 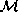 corresponds to a homotopically distinct way
of reaching A from a fiducial point of M, and we can choose the
fiducial point to lie on
corresponds to a homotopically distinct way
of reaching A from a fiducial point of M, and we can choose the
fiducial point to lie on 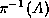 . The projection
. The projection 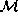 , restricted
to any single copy of A, is an isometry.
, restricted
to any single copy of A, is an isometry.
Since the open neighborhood U of 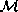 is chosen to be simply
connected and M itself is not simply connected, U will be covered
by multiple copies of itself in
is chosen to be simply
connected and M itself is not simply connected, U will be covered
by multiple copies of itself in 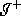 , which will therefore have
multiple asymptotic regions. Let
, which will therefore have
multiple asymptotic regions. Let  be one of
these copies, an open connected neighborhood of a single asymptotic
region of
be one of
these copies, an open connected neighborhood of a single asymptotic
region of 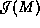 . Construct a partial conformal completion
. Construct a partial conformal completion
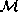 by adjoining a single copy
of
by adjoining a single copy
of 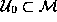 to
to 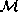 . Then
. Then 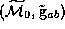 , with
one asymptotic region singled out, satisfies the requirements of the
Lemmas.
, with
one asymptotic region singled out, satisfies the requirements of the
Lemmas.
Suppose the theorem is false. Then there is a causal curve 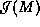 in
M, from
in
M, from 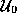 to
to 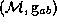 that traverse the topological structure, which is not deformable to
that traverse the topological structure, which is not deformable to
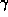 relative to
relative to 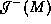 which do not traverse the topological structure. The curves
which do not traverse the topological structure. The curves 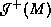 and
and
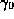 can be lifted to curves
can be lifted to curves 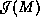 and
and 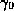 in
in 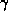 that meet the same point of
that meet the same point of 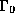 . Because the construction of
. Because the construction of
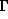 assigns distinct points to homotopically different ways of
reaching the same point of M, the curves
assigns distinct points to homotopically different ways of
reaching the same point of M, the curves 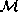 and
and 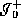 will
join
will
join 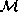 to different copies of the asymptotic
region
to different copies of the asymptotic
region 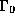 . Because
. Because 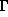 lies in the simply connected
neighborhood U of
lies in the simply connected
neighborhood U of 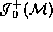 ,
, 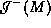 will lie in the
neighborhood
will lie in the
neighborhood 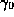 of
of 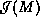 , while
, while 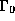 will join
will join 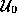 to another copy of U. In this
second asymptotic region, surfaces are outer trapped with respect to
to another copy of U. In this
second asymptotic region, surfaces are outer trapped with respect to 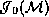 as it is surrounded by an inner trapped surface in the original space (M, not
as it is surrounded by an inner trapped surface in the original space (M, not 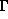 )
)
These large spheres appear outer
trapped as seen from the first asymptotic region, 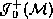 .
Let
.
Let 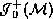 be the covering space of a
Cauchy surface
be the covering space of a
Cauchy surface 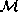 of M and let
of M and let 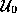 be a sphere in an
asymptotic region of
be a sphere in an
asymptotic region of 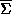 different from the one
containing
different from the one
containing  . If we define outer-directed curves from any
sphere
. If we define outer-directed curves from any
sphere 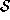 to be those that reach
to be those that reach 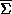 without
intersecting
without
intersecting 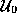 a second time, then the outer directed curves
from
a second time, then the outer directed curves
from 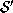 are curves from its concave surface --- curves that
would ordinarily be called inner directed by an observer in the
asymptotic region near
are curves from its concave surface --- curves that
would ordinarily be called inner directed by an observer in the
asymptotic region near 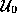 . As
. As 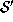 is causal, this
implies that there are strongly outer trapped surfaces that intersect
is causal, this
implies that there are strongly outer trapped surfaces that intersect
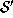 . But this contradicts Lemma 2. Hence any
causal curve
. But this contradicts Lemma 2. Hence any
causal curve 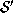 from
from 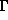 to
to 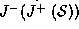 must be
deformable to
must be
deformable to  .
.