 ,
,
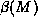 and
and
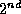 , by
analogy with the six lepton:
, by
analogy with the six lepton: 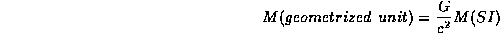 ,
, 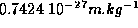 and
and 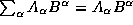 .
.
Varnière Peggy
Exchange Student
Particle Physics Assignment:
The quarks model
The quarks model was presented in 1964 by Gell-Mann and Zweig. They say that the behavior of the hadron known can be explain by the existence of more fundamental particles: the quarks. At this time it was u( up), d( down) and s( strange) only.
This model since this time had been improved like with the discovery of new quarks c( charm), b( bottom or beauty) and t( top) more recently. Some experimental result can be considered as evidenced for the reality of the quarks which, like all the theory in physics, need to be agreed by experiment. For the moment the only way to know the presence of quarks is to see their effects. Indeed the strong interaction causes them to never be alone, or in a theoretical plasma quark-gluons.
In this paper I will, first recall briefly some aspect of this model, and then take some characteristic of the quarks theory like the multiplet structure of the mesons and baryons or the color degree of freedom and try to show how this can be proved by experiment and therefore validate the quarks model.
Since the begin of science physicists always research the
elementary particles. The atom was the most elementar piece
of matter known during a long time. Between the end of the
last century and the first half of this one the electron and
nucleons were discovered. This change how we see the
matter. But since about forty years a new model for the
structure of matter, called quarks model, were appear and
nucleons are no longer elementary particles. It is the leptons
and the quarks. The six quarks are grouped in three family:
 ,
,
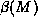 and
and
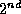 , by
analogy with the six lepton:
, by
analogy with the six lepton: 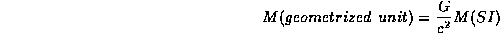 ,
, 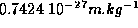 and
and 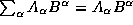 .
.
The quarks model is based on the properties of this six quarks
which are fermion of spin  and therefore obey to the
Pauli principle.
and therefore obey to the
Pauli principle.
Table: some characteristic of the six quarks
In the table ![]() there are the isospin I,
there are the isospin I,
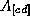 its projection, the strangeness S, the baryon number
B and charge Q of the six quarks u,d,s,c,b,t. Note that
for the four last quarks( s,c,b,t) there is a quantum number
associated with their flavour, like the strangeness for s,
the c quarks has C=1, the b quarks B=-1 and the t
quarks T=1. Such quantities are conserved in the
electromagnetic and strong interaction but violated in the
weak.
its projection, the strangeness S, the baryon number
B and charge Q of the six quarks u,d,s,c,b,t. Note that
for the four last quarks( s,c,b,t) there is a quantum number
associated with their flavour, like the strangeness for s,
the c quarks has C=1, the b quarks B=-1 and the t
quarks T=1. Such quantities are conserved in the
electromagnetic and strong interaction but violated in the
weak.
With the developpement of the model a new quantum number
appear: the color( Red, Blue, Green). It is an intrinsic
degree of freedom of the quarks( all of them can exist equally
in each color![]() ). The color is
responsible for the strong interaction, which cause the quarks
to be never alone. This interaction is mediated by the
gluons which carry a combinaison of color/anticolor. There are
eight of this gluons. In a hadrons there are the valence
quarks (3 in a baryon and 2 in a meson) but there is alo what
we call the sea quarks which come from quantum
fluctuation (interaction between the quarks). Because of this
feature it is difficult to know the mass of the quarks for
example. There are always several quarks all around. The
strong interaction is the reason why we cannot observe free
quarks. But in spite of it there are some experiment to show
the reality of this model.
). The color is
responsible for the strong interaction, which cause the quarks
to be never alone. This interaction is mediated by the
gluons which carry a combinaison of color/anticolor. There are
eight of this gluons. In a hadrons there are the valence
quarks (3 in a baryon and 2 in a meson) but there is alo what
we call the sea quarks which come from quantum
fluctuation (interaction between the quarks). Because of this
feature it is difficult to know the mass of the quarks for
example. There are always several quarks all around. The
strong interaction is the reason why we cannot observe free
quarks. But in spite of it there are some experiment to show
the reality of this model.
The multiplet structure of the baryons known in 1964 is at the origin of the quarks model so it is normal that it fit with experiment. But since this period we have discovered more particles. One of the reason for such discovery was the theoretical prediction from the model( like it was done for the Mendeleiv table at the begin of the century).
One remarkable things about this model is that it predict
all the state we have in nature and just this
one. There is an exact correspondance between the prediction
and the observation. We don't see state not predict by the
quark model and all the state predict by the model are
observed. A such good agrement between what we observed and
the model make our belief in the quarks model stronger. Until
now no state appear to be not predicted![]() .
.
The quarks model is approximatively 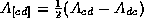 ,
approximatively because the mass of the strange quark is more
important than the mass of the doublet formed by the up and
down quarks and also there are three other quarks which are
really heavier (see table
,
approximatively because the mass of the strange quark is more
important than the mass of the doublet formed by the up and
down quarks and also there are three other quarks which are
really heavier (see table ![]() )
)

Table: quarks masses( sea quarks)
and therefore have a small influence (very massive state). However it is a very good approximation.
The mesons have a spin-parity 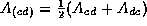 therefore the
simplest way to construct one is to use a quarks and an
antiquarks:
therefore the
simplest way to construct one is to use a quarks and an
antiquarks:  . In order to have a colorless
meson this quarks must be color-anticolor
. In order to have a colorless
meson this quarks must be color-anticolor![]() As regards the baryon they have a baryon number
B=1 then the most economic way is to put together three
quarks each with a different color because of the Pauli
principle but also in order to have a colorless baryon( also
called a color singlet by analogy with the other quantum
number).
As regards the baryon they have a baryon number
B=1 then the most economic way is to put together three
quarks each with a different color because of the Pauli
principle but also in order to have a colorless baryon( also
called a color singlet by analogy with the other quantum
number).
To discuss this in more detail we need to use the group's
formalism. In this notation we have the mesons represent
by  in other words it is one of the
three quarks and one of the three antiquarks. The product of
this representation leads to the decomposition
in other words it is one of the
three quarks and one of the three antiquarks. The product of
this representation leads to the decomposition![]()
 . The quarks model is
validated by the fact that experimentally the mesons are found
to belong to
. The quarks model is
validated by the fact that experimentally the mesons are found
to belong to  octet and singlet.
For the baryon state( qqq) we have
octet and singlet.
For the baryon state( qqq) we have  . The combinaison of three quarks
give a singlet, two octet and a decuplet. Which is the
observed structure for the baryons.
The hadron( mesons and baryons) spectrum is, in a good
approximation, well explain by the
. The combinaison of three quarks
give a singlet, two octet and a decuplet. Which is the
observed structure for the baryons.
The hadron( mesons and baryons) spectrum is, in a good
approximation, well explain by the  symmetry. Even if
it is broken it gives quites good result. Such a great
agreement between the quarks model and the experimental result
is a good point for the reality of quarks.
symmetry. Even if
it is broken it gives quites good result. Such a great
agreement between the quarks model and the experimental result
is a good point for the reality of quarks.
But to be accepted a model need more than that. We have,
in order to assure the real exisence of quarks, to
confront more feature of quarks and their implication to the
experiment. After the model with 3 quarks physicists research
a fourth quarks, just based on the analogy with the
lepton![]() In 1970 it is theoretically shown that a
massive quarks, the c, can explain the absence of the
channel decay
In 1970 it is theoretically shown that a
massive quarks, the c, can explain the absence of the
channel decay 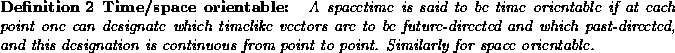 which was not
observed. This theoretical idea guide the experimentalist in
their quest of the c quarks, or more exactly of a bound
state
which was not
observed. This theoretical idea guide the experimentalist in
their quest of the c quarks, or more exactly of a bound
state  . The
. The  was discovered in 1974
in an electron-positron collider. But this discovery causes
more question. Indeed this states(
was discovered in 1974
in an electron-positron collider. But this discovery causes
more question. Indeed this states(  and an excited state
and an excited state
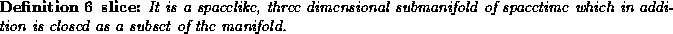 ) have a very narrow width compare to what one
can expect for such massive mesons( masses of 3100MeV for
the
) have a very narrow width compare to what one
can expect for such massive mesons( masses of 3100MeV for
the 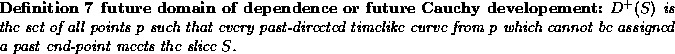 and 3700MeV for the
and 3700MeV for the
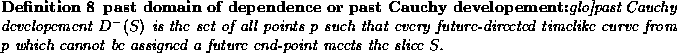 ). Comparatively the discovery of the b
quarks was unexpected. No theory predict a fifth quarks and it
leads to the prediction of a sixth quarks, the top. The bound
state
). Comparatively the discovery of the b
quarks was unexpected. No theory predict a fifth quarks and it
leads to the prediction of a sixth quarks, the top. The bound
state 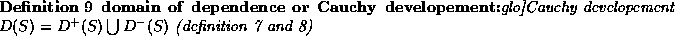 , name
, name 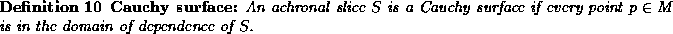 has the same feature
than the
has the same feature
than the  about the spectra and the narrowness
of the width.
about the spectra and the narrowness
of the width.
The narrow width can be explain by the fact that there is no
easy channel. Indeed the decay  is forbiden by energy( the mass of the
is forbiden by energy( the mass of the
 are above the energy of the
are above the energy of the  )
and the only decay is through an OZI-forbiden
channel
)
and the only decay is through an OZI-forbiden
channel![]() . This decay use 3 gluons which give a
very narrow width(
. This decay use 3 gluons which give a
very narrow width(  appear at each vertex
and for this masses
appear at each vertex
and for this masses  is big!).
is big!).
This bound state of a quark and an anti-quarks are also a good
illustration of the quarkonium structure. This name come
from the analogy with the positronium state( a bound state of
an electron and a positron). Below the threshold
( for the
for the  and
and 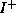 for the
for the
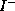 ) the energy level of the charmonium and bottomonium
are very similar to the one for the positronium except for the
energy scale( the 2 quarks are really more
massives see table
) the energy level of the charmonium and bottomonium
are very similar to the one for the positronium except for the
energy scale( the 2 quarks are really more
massives see table ![]() ). Theoretically we don't
know the potential in which the quarks move but we can found
one which fit with the experimental data like
). Theoretically we don't
know the potential in which the quarks move but we can found
one which fit with the experimental data like
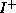 One term like the Coulomb potential with a factor
One term like the Coulomb potential with a factor
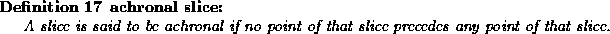 which come from the color( the quarks and gluons
have color but the hadron observed are color singlet), a
confinement potential and the two term which correspond to the
fine and hyperfine structure. But the quarkonium system is,
like the positronium, a bound state of a fermion and an
anti-fermion. It was therefore waited that they have the same
general structure. And it is was is observed (below the
threshold). Above the threshold for the
which come from the color( the quarks and gluons
have color but the hadron observed are color singlet), a
confinement potential and the two term which correspond to the
fine and hyperfine structure. But the quarkonium system is,
like the positronium, a bound state of a fermion and an
anti-fermion. It was therefore waited that they have the same
general structure. And it is was is observed (below the
threshold). Above the threshold for the  and the
and the
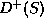 the channel priviledged by OZI-rule is now also
allowed by energy and the width of the state become bigger(
for the
the channel priviledged by OZI-rule is now also
allowed by energy and the width of the state become bigger(
for the 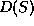
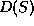 to compare the
to compare the
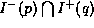
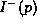 the mass difference is small, but
it is enough to go through the threshold).
the mass difference is small, but
it is enough to go through the threshold).
Another feature of the quarks is the fact that they have
fractionnal charge( see table ![]() ). Such thing
was never observed in nature and the charge of the electron
e is the common unit of electric charge( and all the
observable free particles have an integer charge in this
unit). But the fact that the strong interaction prevent the
quarks to be alone agree with this none direct observation of
fractionnal charge. However it is possible to detect the
presence of fractionnal charge by its effect, which is the
only method we have, for the moment, to show the reality of
the quarks model. But first let begin by the
most simple verification and by consequence the most
fundamental, if this does not work we know that the theory is
false! If we take the
). Such thing
was never observed in nature and the charge of the electron
e is the common unit of electric charge( and all the
observable free particles have an integer charge in this
unit). But the fact that the strong interaction prevent the
quarks to be alone agree with this none direct observation of
fractionnal charge. However it is possible to detect the
presence of fractionnal charge by its effect, which is the
only method we have, for the moment, to show the reality of
the quarks model. But first let begin by the
most simple verification and by consequence the most
fundamental, if this does not work we know that the theory is
false! If we take the 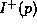 approximation for the
composition of baryon then we can compute the charge that this
imply for the baryon with
approximation for the
composition of baryon then we can compute the charge that this
imply for the baryon with 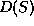
![]() because here we confine
our attention on uds. for example for the proton we have
because here we confine
our attention on uds. for example for the proton we have
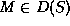 and it works for all the
hadrons. The mesons have a net charge 0 which is also in
agrement with this formula. This formula, called Gell-Mann and
Nishijima formula, is based on the observation. It link the
fractionnal charge with the baryon number of quarks
and it works for all the
hadrons. The mesons have a net charge 0 which is also in
agrement with this formula. This formula, called Gell-Mann and
Nishijima formula, is based on the observation. It link the
fractionnal charge with the baryon number of quarks
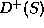 . All the known hadrons properties are well
explain by this model and therefore we can see in more detail
how to, experimentally, show the reality of fractionnal charge.
. All the known hadrons properties are well
explain by this model and therefore we can see in more detail
how to, experimentally, show the reality of fractionnal charge.
An experimental way for that is to use the vector mesons
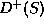 ,
, 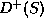 ,
, 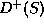 ( see table
( see table ![]() ).
).
Table: leptonic width of the vector mesons
We take the leptonic width of this vector meson( in fact it
is possible also with the  and
and 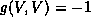 but they
also have special feature because of their high masses, about
this see
but they
also have special feature because of their high masses, about
this see
![]() ). The leptonic width
). The leptonic width  of the
reaction
of the
reaction 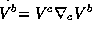 where
where
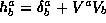 represent a lepton can be calculated from the
Feymann diagram
represent a lepton can be calculated from the
Feymann diagram ![]()
we have at the quarks-photon
vertex 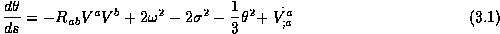 with
with  the
weight of the quarks in meson,
the
weight of the quarks in meson, 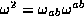 its charge and
its charge and
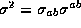 the electromagnetic coupling strength. At the
photon-lepton vertex we have
the electromagnetic coupling strength. At the
photon-lepton vertex we have 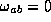 . This lead to the
approximativ formula
. This lead to the
approximativ formula 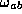 . The factor
. The factor 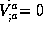 is the experimental way to verify the fractionnal charge of
quarks. And from the result we see that the fractionnal charge
is approved by the experiment.
is the experimental way to verify the fractionnal charge of
quarks. And from the result we see that the fractionnal charge
is approved by the experiment.
Another experimental fact which show as the same time the
validity of the fractionnal charge and the color degree of
freedom is the life-time of the
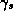 .
. 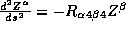 In order to decay we need that q and
In order to decay we need that q and 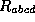 have the
same color and also the same charge( the photon carry no
charge!). So we can made an analogy with the
have the
same color and also the same charge( the photon carry no
charge!). So we can made an analogy with the
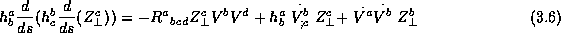 but there is a slightly
difference because of the fractionnal charge! Indeed not all
of the antiquarks can anhilate a quarks (to annhilate, say
u, we need an antiquarks of charge
but there is a slightly
difference because of the fractionnal charge! Indeed not all
of the antiquarks can anhilate a quarks (to annhilate, say
u, we need an antiquarks of charge  so there
are
so there
are  possible and
not the six quarks). This imply a factor
possible and
not the six quarks). This imply a factor 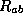 in the
calculation and this is experimentally verify.
in the
calculation and this is experimentally verify.
Physics is an experimental science. All theory need to be
agreed by experiment in order to be accepted. When appear the
fact that the  was composed of uuu, three
indentical fermions in the same quantum state, the solution
found in order to keep the Pauli princuple was that the quarks
carry another quantum number called color. It is obvious that
this color appear, at this time, like a magic
trick to save the quark model. But in order to agree with the
experiment this tri-value quantum number was required. And at
the same time it explain why the only state are
was composed of uuu, three
indentical fermions in the same quantum state, the solution
found in order to keep the Pauli princuple was that the quarks
carry another quantum number called color. It is obvious that
this color appear, at this time, like a magic
trick to save the quark model. But in order to agree with the
experiment this tri-value quantum number was required. And at
the same time it explain why the only state are
 and qqq: need to be a color singlet.
and qqq: need to be a color singlet.
The mathematical model for the color degree of freedom is
 but, unlike for the flavor, it is an exact symmetry
for the color( there are just 3 colors R,B,G).
but, unlike for the flavor, it is an exact symmetry
for the color( there are just 3 colors R,B,G).
There is one experience where one can see the presence
of fractionnal charge and at the same time this experiment is
use to validate the idea of color. The idea is to plot the
ratio R of the cross-section of 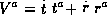 and
and 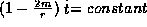
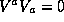
The first one is in fact 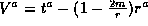 and, because of the strong interaction. When
and, because of the strong interaction. When
 fall apart there is creation of hadrons( the
strong force between quarks is about 7 pions per fermi). The
second one is just electromagnetic interaction for which we
have very good approximation.
fall apart there is creation of hadrons( the
strong force between quarks is about 7 pions per fermi). The
second one is just electromagnetic interaction for which we
have very good approximation.
If color exist there must be a factor of three that appear in
the calculation. We have 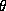 . If we do the same calculation for
the
. If we do the same calculation for
the 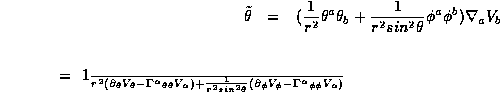 final state we have to take into account
the fractionnal charge of the quarks(
final state we have to take into account
the fractionnal charge of the quarks( 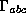 ,
,
 ...) and also the color( just multiply by three
for each color).
...) and also the color( just multiply by three
for each color).  . Everything cancel
out except the color and charge part. we found then
. Everything cancel
out except the color and charge part. we found then
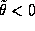 whereas is color is meaning less
whereas is color is meaning less
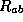 . The experimental plot is clear! The right
answer is the one which take into account the color degree of
freedom and the fractionnal charge.
. The experimental plot is clear! The right
answer is the one which take into account the color degree of
freedom and the fractionnal charge.
Another experiment which show the reality of the color as
quantum number of the quarks is the life-time of the
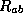 .
. 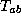 seen before for the fractionnal
charge. All the quarks, because of color,have three
possibilities of existence. For example a quarks, say d, can
be
seen before for the fractionnal
charge. All the quarks, because of color,have three
possibilities of existence. For example a quarks, say d, can
be  or
or 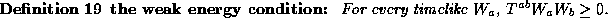 . So the amplitude is
multiply by three and like it is square there is a factor of
nine. This factor is actually seen in the experimental
result and this give agrement between experiment and theory.
. So the amplitude is
multiply by three and like it is square there is a factor of
nine. This factor is actually seen in the experimental
result and this give agrement between experiment and theory.
In the same way, collision 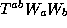 is a collision
is a collision  . It must be identical to the collison
. It must be identical to the collison
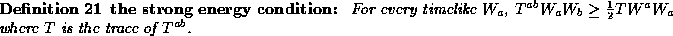 but with the color degree of freedom. Because of
the color the
but with the color degree of freedom. Because of
the color the  can be anhilated if,
and only if, they carry a couple color/anticolor. For example
a quarks, say
can be anhilated if,
and only if, they carry a couple color/anticolor. For example
a quarks, say  , can be anhilated only with a
, can be anhilated only with a
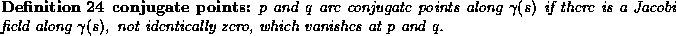 . This restriction cause the ratio to be
reduced by three compare to the one from
. This restriction cause the ratio to be
reduced by three compare to the one from 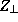 . And it is was is observed
experimentally.
. And it is was is observed
experimentally.
The reality of a theoretical model in physics is proved by the agreement with experimental results. In a such way the quarks model is a good one. There are evidences of the principal features of the model in experiments. And even when we used crude approximations there is a such great agreement with experimental result that we have to believe! even if we cannot see free quarks.
Some other way to prove the reality of quarks are explored. It is the theoretically predicted plasma quark-gluons where the quarks are mixed in a soup. They are so near that they are near free, compare to the strong coupling when they try to get out from one another. If we can observed such a plasma then the quark model will be strongly validate.