SUBJECT MATTER

Classical mechanics embraces an unusually broad range of topics, far more than can be discussed during this term. Classical mechanics addresses basic problems ranging from motion of astronomical bodies to nuclear and particle physics, for velocities ranging from zero to the velocity of light, from one-body to statistical many-body motion, and extensions to quantum mechanics. The roadmap given below illustates that the foundations of classical mechanics were first established during the seventeenth century by Newton and Galileo; this approach is called Newtonian mechanics. The essential physics contained in the Newtonian formulation of classical mechanics is contained in Newton's three laws of motion. The Newtonian formulation is the most intuitive approach to classical mechanics in that it is based on vector quantities like force, momentum, acceleration, etc, which are easy to visualize, while the theory has embedded into it both cause and effect.

Lagrange, Euler, Hamilton, and Jacobi developed powerful analytical formulations of classical mechanics during the eighteenth and nineteenth centuries. These alternative analytical approaches are based on ideas of least action and variational principles as suggested by Liebnitz contemporaneously with Newton. The Lagrangian formulation is cast in terms of kinetic and potential energies, that involve only scalar functions, and the philosophical belief is that the physical universe follows paths through time and space that are extrema. The powerful Hamiltonian and Hamilton-Jacobi formulations of classical mechanics are closely related to the Lagrange formulation. These variational formulations provide the only viable approach to solving many-body systems. For over two centuries the Newtonian formulation reigned supreme in classical mechanics. It was only in 1905 that the full significance and superiority of the variational formulations of classical mechanics became widely accepted. The Theory of Relativity requires that the laws of nature are invariant to the reference frame. This is not satisfied by the Newtonian formulation of mechanics which assumes one absolute frame of reference and a separation between space and time. In contrast, the Lagrangian and Hamiltonian formulations of the principle of least action remain valid in the Theory of Relativity once the Lagrangian is written in an invariant form. The complete invariance of the variational approach to coordinate frames is precisely the formalism necessary for relativistic mechanics. The Poisson bracket and Hamilton-Jacobi formulations of Hamiltonian mechanics naturally incorporate the underlying physics of quantum mechanics and quantum field theory. As a consequence, the philosophical opposition to the variational approach, which some considered to be speculative and "metaphysical", no longer exists and now it has become the supreme and most useful formulation of classical mechanics as well as quantum physics and statistical mechanics.

Although quantum physics has played a dominating role in the development of physics during much of the past century, classical mechanics still is a vibrant field of physics that recently has led to exciting developments associated with chaos theory that has spawned new branches of physics and mathematics as well as changing our notion of causality.

The primary goal of this course is to introduce you to these powerful variational principles that play such a pivotal role in many branches of science and engineering, and, in particular, their use in classical dynamics. A secondary goal is to stimulate, interest, and challenge you at the crucial period when you first encounter the sophistication and challenge of junior/senior courses as well as for developing your problem solving skills. The connections and applications of classical mechanics to modern physics will be emphasized throughout the course. This course will follow the general features of the roadmap shown in the figure and in the syllabus. It will be assumed that you already have taken an introductory course in Newtonian mechanics. Therefore P235W will start with a brief review of the elements of the Newtonian formulation of classical mechanics. This will include a discussion of linear oscillators followed by an introduction to non-linear systems and chaos. The Lagrangian and Hamiltonian formulations of classical mechanics then will be introduced and will form the backbone of the remainder of this course. It will be necessary to introduce variational calculus that underlies the Lagrangian and Hamiltonian formulations. Applications to two-body motion, motion in non-inertial frames, the dynamics of rigid-body motion, and coupled oscillatory systems will be discussed. The course will end with a brief introduction to advanced topics in Hamiltonian physics, the Special theory of Relativity, and the connection between classical mechanics and quantum physics.

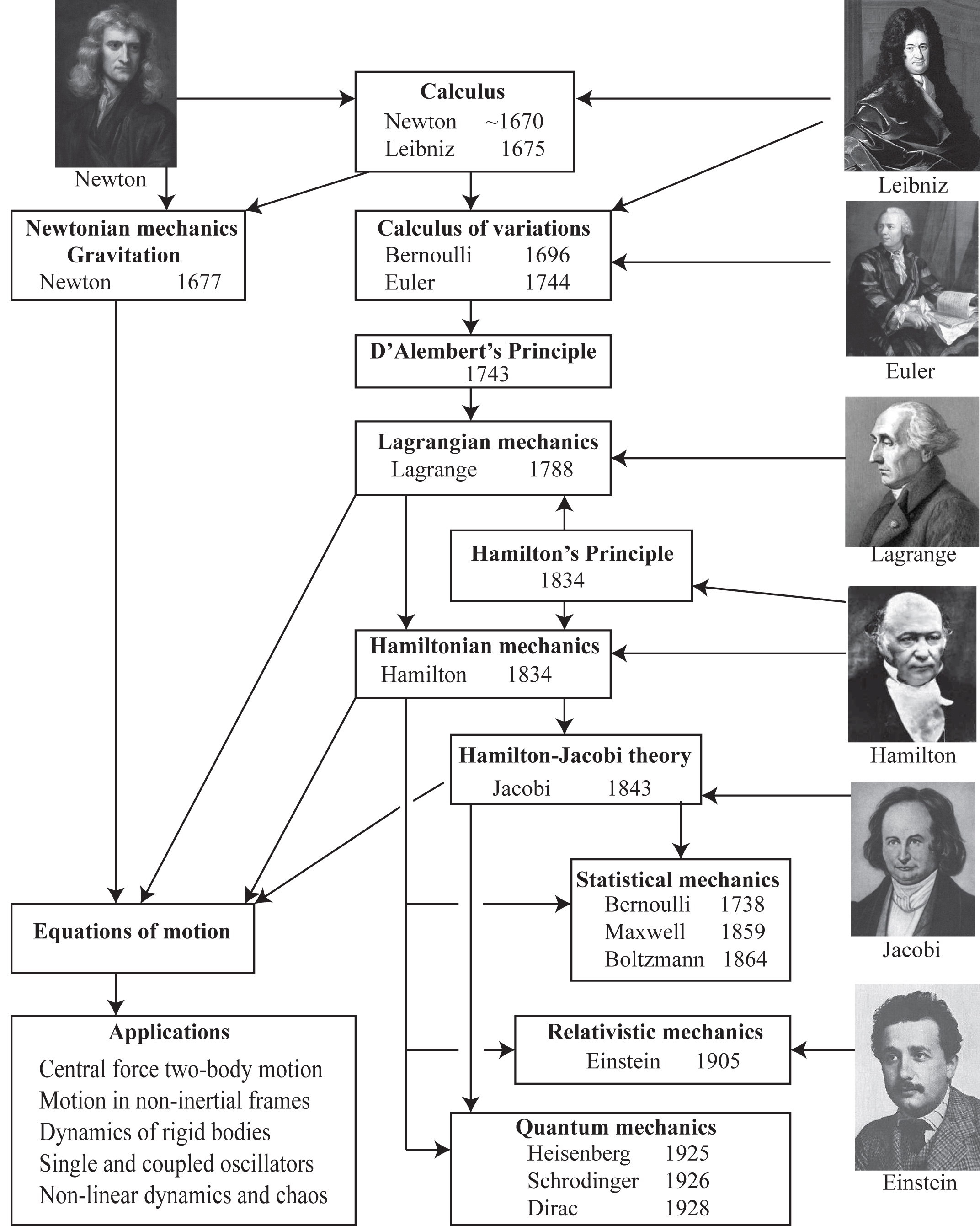
Chronological roadmap of the parallel developments of the Newtonian and the variational approaches to classical mechanics.