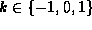In order to simplify the computation we take the case of the
radial geodesics, this means that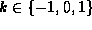 
and k=0
the flat universe. This gives the system:
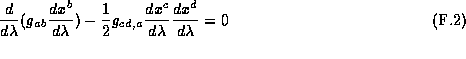
In order to find the timelike vector 
we use the geodesic equations and the fact that 
for timelike vectors.
This gives us
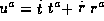
Where c is the constant equal to 
(from the geodesic equation).
Now we compute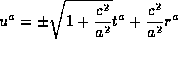 
the covariant derivative of the tangent timelike vector of the geodesics.
One can ask for what c we have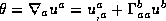 
. For say c>0 one must have
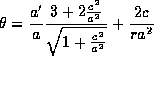
For a flat space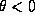 
. It is not possible for this to be true if 
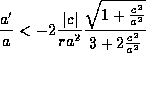. In other words for an universe in expansion 
.
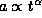If we now take c to be negative then there exist a case of convergence for a flat space with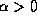 
.