These computations are easier for null geodesic ,as a null vector,
.
We ask for a radial null geodesic of the form
.
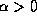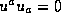
Then one can find that the geodesic equation give us
which give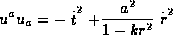 
where d is a constant.
The form of the radial null geodesic is then:
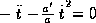
As it is up to a constant we can forget the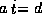 
in the computation of 
.
In order to compute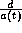 
one used the analogue of what was done for the timelike case.
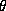
To see if that result makes sense we can just take some of the function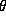 
and compute the value of 
.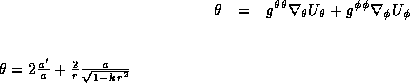