Problem Set 3

Problem Set 3

Due Friday, September 23, by 4pm in the homework locker

Problem 1 [10 points]

Griffiths Problem 1.21
Problem 2 [10 points]

Although the line integral of a gradient is independent of the integration path, the same is not true for an arbitrary vector function. For the function v = y²x̂ + 2x(y+1)ŷ, compute the integral ∫_a^b v·dℓ along path (1), and then along path (2), as shown in the figure below.
Now compute ∮ v·dℓ along the closed loop that consists of going out from point a along parth (1) and returning back to point a along path (2). What do you get?
Problem 3 [10 points]

This problem is meant to help you understand the notion of the flux of a vector field through a surface.
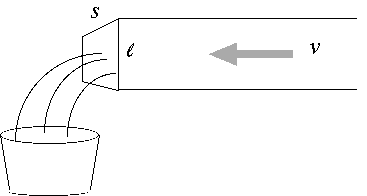
a) Suppose water flows with speed v down a rectangular pipe of crossectional lengths s and ℓ, as shown in the figure below. What is the rate Φ = volume per unit time, at which water accumulates in the bucket?
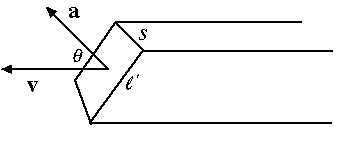
b) Now we slice the end of the pipe off at some angle θ , as in the figure below. This doesn't change Φ of course. Express your formula for Φ in terms of the dimensions s and ℓ' of the end, and the angle of tilt θ.
c) Write teh formulat for Φ more compactly, in terms of the vector area a of the end and the vector velocity v, as shown in the figure below.
d) What if the velocity varied (in magnitude and/or direction) from point to point, and the end of the pipe were cut in some arbitary way, as in the figure below. How would you then compute Φ in this case?
Problem 4 [10 points]

Griffiths Problem 1.54
Problem 5 [10 points]

Griffiths Problem 2.10