By reading the beginning of the article it becomes clear why one
need to study the causal structure (chapter ![]() )
and the energy condition (chapter
)
and the energy condition (chapter ![]() ).
).
The theorem 1, if an asymptotically flat, globally
hyperbolic spacetime 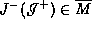 satisfies the averaged
null energy condition , then every causal curve from
satisfies the averaged
null energy condition , then every causal curve from 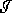 to
to 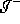 is deformable to
is deformable to 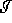 ,
need to be translate in a more common language.
,
need to be translate in a more common language.
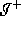
Figure: Penrose diagram of a spacetime which illustrate the topological
censorship. note that the singular region is not fully represent.
First the hypotheses, from the observation it seems to be a
reasonable assumption to take an asymptotically flat space.
The averaged null energy condition, which say that an observer
always measures a cumulative non negative energy density along any curve is agreed by all experiments
done until now.
The only assumption very restrictive is the one of globally hyperbolic (see definition ![]() page
page ![]() ).
).
The existence of a Cauchy surface is not something proved, but nothing is against also. However given the discussion of stably causal spacetimes it is reasonnable.
To see the topology one need to have a causal curve which, passes through the topology and can reach us.
In other words a causal curve is piecewise timelike (path of massive particles) or null (path of zero-mass particles).
This
theorem states that every causal curve from 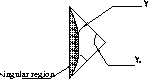 to
to
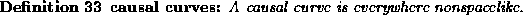 , i.e. all the curve that reach us, are
deformable to
, i.e. all the curve that reach us, are
deformable to 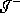 which nevers enter in the
region containing the topology. And, because curves which go through region containing topology
cannot be deformed to ones which do not, we are not able to probe
the topology! It is always behind the horizon of events we see.
which nevers enter in the
region containing the topology. And, because curves which go through region containing topology
cannot be deformed to ones which do not, we are not able to probe
the topology! It is always behind the horizon of events we see.