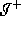 be any
asymptotically flat spacetime with a simply connected Cauchy surface
be any
asymptotically flat spacetime with a simply connected Cauchy surface
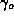 . Let
. Let 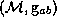 be a smooth closed compact orientable
2-surface in
be a smooth closed compact orientable
2-surface in  . Then no inner directed null geodesic from
. Then no inner directed null geodesic from 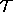 with respect to
with respect to  is part of
is part of 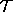 .
.
Lemma 1, Let 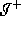 be any
asymptotically flat spacetime with a simply connected Cauchy surface
be any
asymptotically flat spacetime with a simply connected Cauchy surface
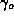 . Let
. Let 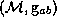 be a smooth closed compact orientable
2-surface in
be a smooth closed compact orientable
2-surface in  . Then no inner directed null geodesic from
. Then no inner directed null geodesic from 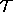 with respect to
with respect to  is part of
is part of 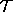 .
.
The figure ![]() can help our understanding of this lemma.
can help our understanding of this lemma.
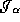
Figure: Representation of the inner and outer directed null geodesics which do not go to the same asymptotically flat region.
It needs also some explanation.
The hypothesis are similar to the one from the theorem explained before except about the simply connected Cauchy surface 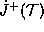 .
Because it is simply connected we have a good definition of inside/outside of the surface.
This is useful to define the inner/outer directed geodesics.
What this lemma say is that we don't need to pay attention to the inner directed null geodesics.
They do not go at the same place as the outer directed ones.
.
Because it is simply connected we have a good definition of inside/outside of the surface.
This is useful to define the inner/outer directed geodesics.
What this lemma say is that we don't need to pay attention to the inner directed null geodesics.
They do not go at the same place as the outer directed ones.
For the lemma 1 we concentrate on one of the asymptotical region which is used to define the inner and outer geodesics. By hypothesis we have a simply connected spacetime.
This give us a well-defined notion of interior/exterior. Which
is important because we want to prove that the inner-directed
geodesics are not interesting for the topological censorship
and that because the inward never enter in the causal future!
Lemma 2, Let  be an
asymptotically flat spacetime that satisfies ANEC and has a simply
connected Cauchy surface
be an
asymptotically flat spacetime that satisfies ANEC and has a simply
connected Cauchy surface  . Then no surface
. Then no surface 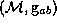 , strongly
outer trapped with respect to
, strongly
outer trapped with respect to  , intersects
, intersects
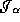 .
.
This mean that someone at 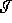 cannot know what is happening on
cannot know what is happening on 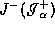 and that because the surface is not in the past of
and that because the surface is not in the past of 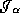 .
.
The lemma 2 is by contradiction and based on point set
topology, like the theorems of the chapter
![]() . We assume that the boundary of the
future of
. We assume that the boundary of the
future of 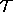 can intersect
can intersect  so there is a
geodesic.
But from the Raychaudhuri equation , like
so there is a
geodesic.
But from the Raychaudhuri equation , like 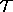 on
on 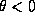 , this geodesic has a finite affine parameter. Therefore it
cannot hit
, this geodesic has a finite affine parameter. Therefore it
cannot hit 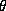 ! So the assumption used is false,
therefore
! So the assumption used is false,
therefore 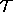 does not intersect
does not intersect 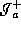 .
.