After the study of the singularity theorem (chapter
) this will be easier!
An important idea in the proof of the topological censorship is the one of covering space . It is the manifold resulting from the unwrapping of the spacetime.
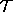
By construction the covering manifold of an asymptotically flat spacetime containing topology has lot of asymptotic
regions. Because of that there are indices a on the
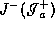. There are several asypmtotical region where curves
can go.
Then by using this idea one can prove the Topological Censorship theorem. This proof is by contradiction
From the orginal spacetime we construct a simply connected cover
.
We have the curves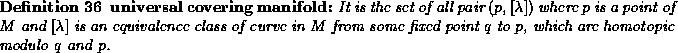 
and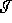 
like in the figure but now in the covering space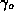 
connects 
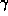to an other asymptotic region.
Large sphere in this region are strongly outer trapped (definition page ) with respect to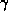 
. Thus it cannot be seen from 
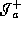(by lemma 2).
Like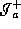 
passes through it, it cannot be seen either. It is the contradiction, therefore we prove that we are not able to probe the topology.