Problem Set 11

Problem Set 11

DQ 11 -- Due Tuesday, April 27, by 5pm

This is a very interesting question that will test how well you understand the difference between a classical gas and a quantum gas of fermions, and a quantum gas of bosons. You should be able to get you answer with a simple graphical analysis, no algebra needed!
Consider a thermodynamic system consisting of two gases in volumes V₁ and V₂, separated by a thermally conducting, freely sliding wall, as shown in the diagram below. The gas in V₁ has N₁ particles, while the gas in V₂ has N₂ particles. Particles cannot pass through the separating wall. The system is in isolation from the rest of the universe, and the total volume V = V₁ + V₂ is fixed. In thermal equilibrium, the pressures of the gases on the two sides of the sliding wall must be equal.

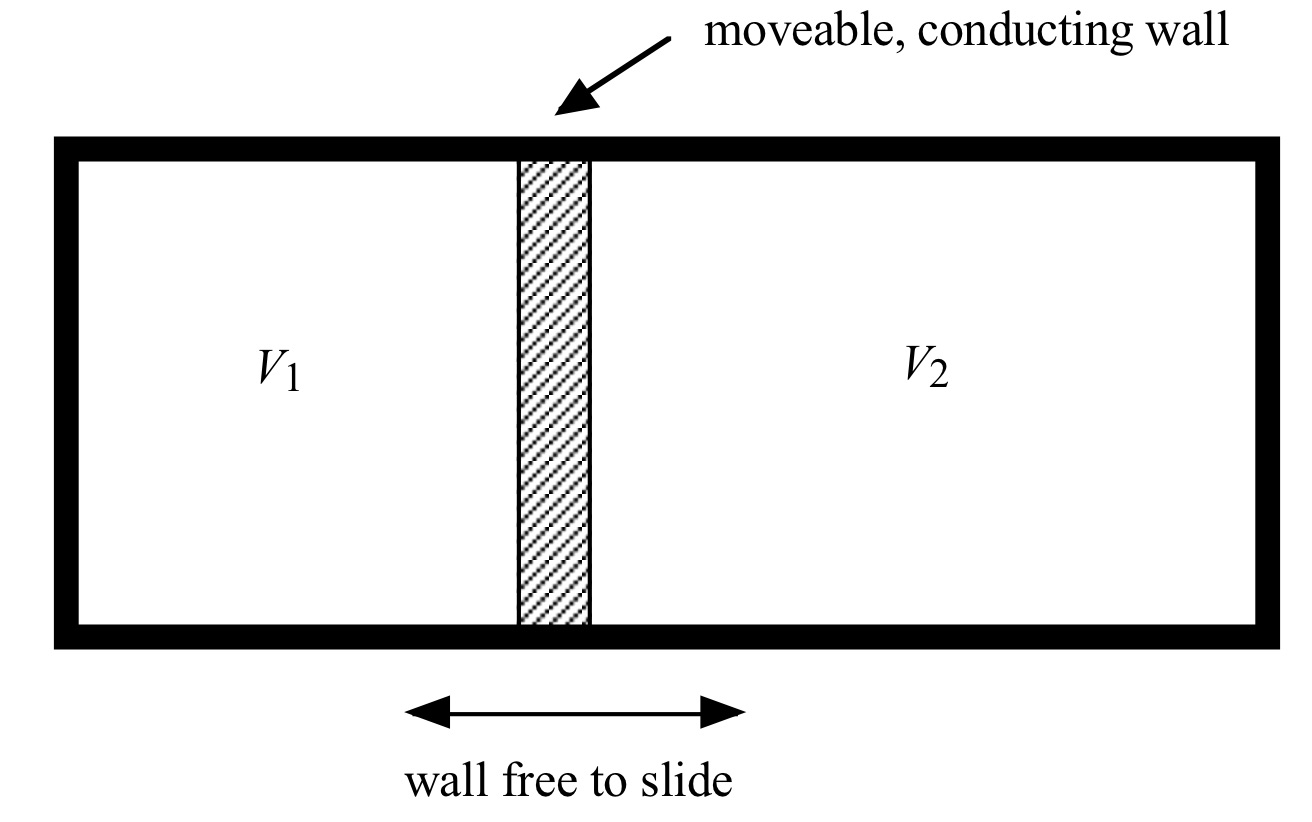
If the system is initially in thermal equilibrium at temperature T, for each case below explain in which direction the wall between the two gases will move if the temperature is increased a small amount ΔT.
a) The gas in V₁ is an ideal gas of fermions in the degenerate limit, i.e. k_BT << ε_F. The gas in V₂ is a classical ideal gas.
b) The gas in V₁ is an ideal gas of bosons in a Bose-Einstein condensed state, i.e. T < T_c. The gas in V₂ is a classical ideal gas.
c) The gas in V₁ is an ideal gas of fermions, and the gas in V₂ is an ideal gas of bosons. However both are now in the non-degenerate limit where their behavior is approaching that of a classical ideal gas (i.e. treat them in the small fugacity limit, keeping only the leading quantum correction to the classical equation of state).

Post your response on the Discussion Board at this link: DQ11
To post your response, click on the Create Thread link on the top of the Discusson Board page.

Problems -- Due Thursday, April 29, by 5pm.

Upload your solutions to Blackboard at this link: PS11

Problem 1 [20 points]
Consider a non-interacting gas of spin zero bosons, whose energy-momentum relationship is given by ε(p) = A|p|^s, for some fixed positive numbers A and s. The dimensionality of the gas is the number d, i.e. the volume of the gas is V = L^d, for a system of length L. In the following parts, we are considering the behavior in the thermodynamic limit of V → ∞.
a) For what values of s and d will there exist Bose-Einstein condensation at sufficiently low temperatures? In particular, show that for s=2 (non-relativistic massive particles) there is no Bose-Eisntein condensation in d=2 dimensions.
b) For the case that there is Bose-Einstein condensation, write an expression that gives how the condensation temperature T_c depends on the total density of particles n, and how the condensate density n_o depends on temperature T.
c) Show that the pressure is related to the energy by, p = (s/d)(E/V)
d) Can a gas of photons in d = 3 undergo Bose-Einstein condensation?
Problem 2 [25 points]
Consider a three-dimensional gas of N indistinguishable non-interacting spin zero bosons of mass m in an external isotropic harmonic potential U(r) = (1/2)mω₀² |r|², where r = (x, y, z). This might be taken as a model for bosons in a magnetic trap. The quantized single particle energy levels are given by ε(n_x, n_y, n_z) = ℏω₀ (n_x + n_y + n_z + 3/2), where n_x, n_y, n_z = 0, 1, 2, . . . are integers.
a) Compute the density of states g(ε). The density of states is such that g(ε)dε is the number of single particle states between ε and ε+dε.
Hint: You should try to do this the same way you found g(ε) in Problem Set 10 problem 2, but generalizing to 3D. You may assume that the thermal energy is much greater than the spacing between the energy levels, i.e. k_BT >> ℏω₀.
b) What is the largest value that the fugacity z can take?
c) Show that this system has Bose-Einstein condensation at sufficiently low temperature.
d) Find the Bose-Einstein condensation temperature T_c as a function of the number of paricles N.
e) Find how the number of particles N₀(T) in the condensed state varies with temperature for T=0 to T_c.