Problem Set 3

Problem Set 3

DQ 3 -- Due Tuesday, February 23, by 5pm

Consider a box containing N extremely relativistic particles, moving so fast that their speed can be taken as the speed of light c, but the relativisitc factor γ = 1/(1-v²/c²)^1/2 is finite. For such particles the energy-momentum relation is well approximated by ε = pc. Equivalently, you can think of these as massless particles (think photon!) which travel with speed c, carry momentum p, and have energy ε = pc.
Using a kinetic theory for such particles, as in Notes 2-1, find the relation between the pressure P, volume V, number of particles N, and the average energy per particle <ε>. You should assume that a particle is equally likely to be traveling in any spatial direction. If we assume that the ideal gas law continues to hold for such a gas (it does), what is the relation between the average energy per particle and the temperature?

Post your response on the Discussion Board at this link: DQ3
To post your response, click on the Create Thread link on the top of the Discusson Board page.

Problems -- Due Thursday, February 25, by 5pm.

Upload your solutions to Blackboard at this link: PS3

Problem 1 [20 points total]
A thermodynamic engine can be thought of as a cyclic process by which heat (TdS) pumped from a "hot" reservoir into a system (the engine) is converted into mechanical work (pdV) done by the engine. The most famous such example is the Carnot cycle. Another such cycle is the Otto cycle, schematically shown in the diagram below as a directed path in the volume-entropy plane. The Otto cycle is a rough approximation to the operation of a gasoline engine.

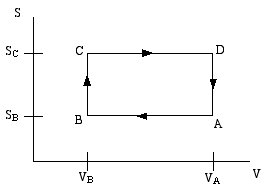
The gas is compessed adiabatically (constant entropy) in the step A to B. Then it is heated isochorically (constant volume) in the step B to C (this step corresponds to the combustion of the gas in the gas engine). The gas is then expanded adiabatically in step C to D (this is the power stroke). Finally the gas is cooled isochorically to bring it back to its initial state; this is step D to A.
Step B to C extracts heat Q_BC from the "hot" reservoir to heat the gas, while step D to A returns heat Q_DA = − Q_AD to the "cold" reservoir (usually the ambient atmosphere). The difference is the work done by the engine.
If the engine efficiency is defined as ratio of the net heat converted to work, divided by the heat withdran from the hot reservoir
ε = (Q_BC − Q_AD)/Q_BC
then assuming the gas is an ideal gas, show that the efficiency of the Otto cycle is given by,
ε = 1 − (V_B/V_A)^{(C_p − C_V)/C_V}
Problem 2 [15 points total]
Consider a box of volume V. The box is split exactly in half by a thermally conducting imovable wall. Equal quantities of the same type of ideal gas fill each half of the box, and the system is in equilibrium. The total energy of the gas is fixed at E_T.
a) Show that the pressure of the gas on each side is the same (remember, the wall is imovable, so you can't just appeal to mechanical equilibrium).
b) Using the formular derived in lecture for the number of states Ω(E) of an ideal gas at total energy E, find the most likely value for the energy of the gas on one side of the box.
c) Using Ω(E), if P(E) is the probability distribution for the gas on one side of the box to have energy E, show that the relative width (i.e. the width divided by the average) of P(E) is proportional to 1/N^1/2, for sufficiently large N, where N is the number of particles in the gas. This shows that the fluctuation of E away from its average becomes negligibly small in the thermodynamic limit of N going to infinity. (For "width" you may use half width at half height or any other reasonable definition.)