Problem 1 [15 points]
This is a very interesting question that will test how well you understand the difference between a classical gas and a quantum gas of fermions, and a quantum gas of bosons. You should be able to get you answer with a simple graphical analysis, no algebra needed!
Consider a thermodynamic system consisting of two gases in volumes V1 and V2, separated by a thermally conducting, freely sliding wall, as shown in the diagram below. The gas in V1 has N1 particles, while the gas in V2 has N2 particles. Particles cannot pass through the separating wall. The system is in isolation from the rest of the universe, and the total volume V = V1 + V2 is fixed. In thermal equilibrium, the pressures of the gases on the two sides of the sliding wall must be equal.
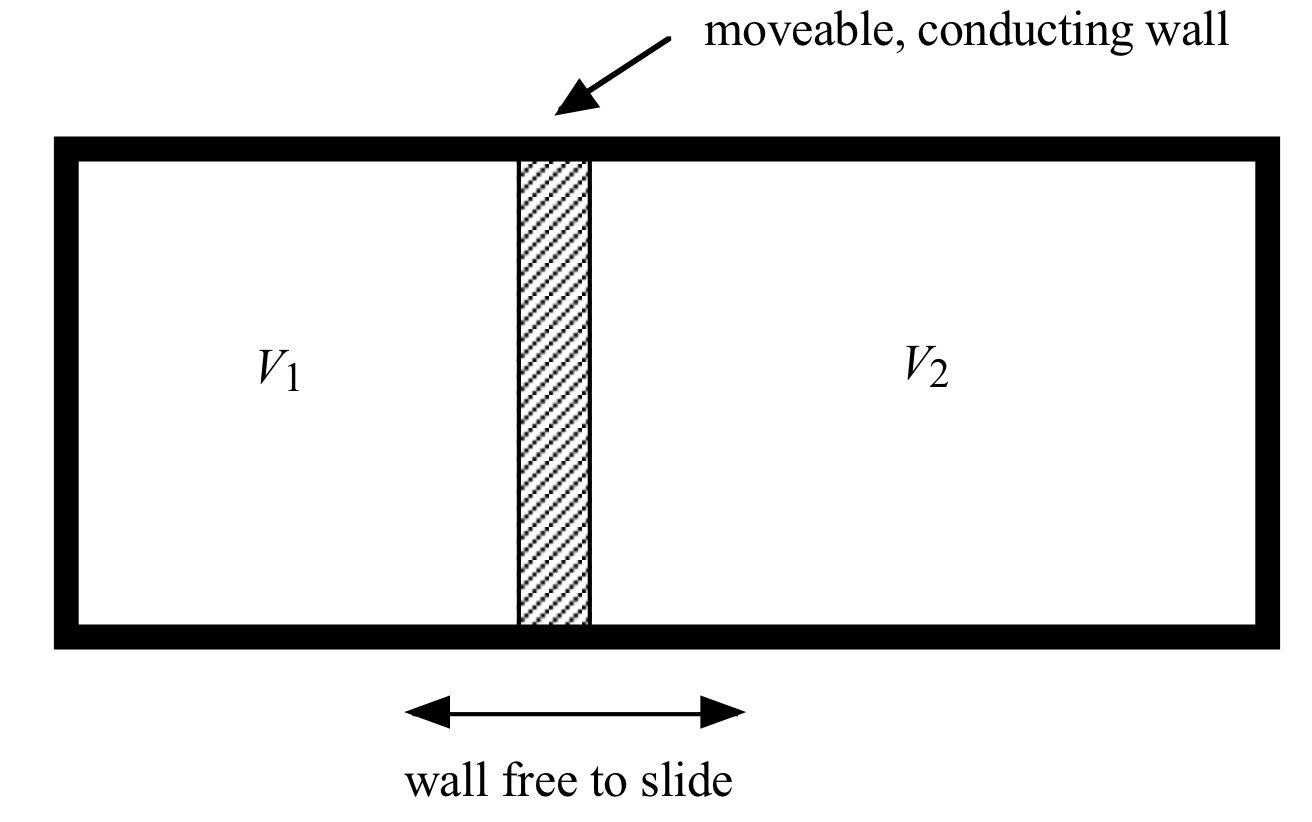
If the system is initially in thermal equilibrium at temperature T, for each case below explain in which direction the wall between the two gases will move if the temperature is increased a small amount ΔT.
a) The gas in V1 is an ideal gas of fermions in the degenerate limit, i.e. kBT << εF. The gas in V2 is a classical ideal gas.
b) The gas in V1 is an ideal gas of bosons in a Bose-Einstein condensed state, i.e. T < Tc. The gas in V2 is a classical ideal gas.
c) The gas in V1 is an ideal gas of fermions, and the gas in V2 is an ideal gas of bosons. However both are now in the non-degenerate limit where their behavior is approaching that of a classical ideal gas (i.e. treat them in the small fugacity limit, keeping only the leading quantum correction to the classical equation of state).
Problem 2 [20 points]
Consider a non-interacting gas of spin zero bosons, whose energy-momentum relationship is given by ε(p) = A|p|s, for some fixed positive numbers A and s. The dimensionality of the gas is the number d, i.e. the volume of the gas is V = Ld, for a system of length L. In the following parts, we are considering the behavior in the thermodynamic limit of V → ∞.
a) For what values of s and d will there exist Bose-Einstein condensation at sufficiently low temperatures? In particular, show that for s=2 (non-relativistic massive particles) there is no Bose-Eisntein condensation in d=2 dimensions.
b) For the case that there is Bose-Einstein condensation, write an expression that gives how the condensation temperature Tc depends on the total density of particles n, and how the condensate density no depends on temperature T.
c) Show that the pressure is related to the energy by, p = (s/d)(E/V)
d) Can a gas of photons in d = 3 undergo Bose-Einstein condensation?