Problem Set 11

Problem Set 11

Problems -- Just for Fun!!
You do not have to turn these in, and they will not be graded!

Problem 1 [15 points]
Consider a point charge q at rest at the origin in an inertial frame 𝒦'. We know the electric and magnetic fields E'(r', t') and B'(r', t') of the charge in this frame 𝒦'. The frame 𝒦' is moving with velocity v in the +x direction, as seen by an observor in the inertial frame 𝒦. Using the Lorentz transformation for the electromagnetic fields, find the electric and magnetic fields of the charge as seen by the observor in frame 𝒦.
Show that the fields you get above are the same as we found from the Lienard-Wiechert potentials as applied to the case of a charge moving with constant velocity v, see Eqs. (6.1.58) and (6.1.59) in Notes 6-1. Remember, you have to transform both the fields and the coordinates, i.e. your result should give E(r,t) and B(r,t).
Problem 2 [20 points]
Consider a flat conducting sheet lying in the xy-plane at z=0. The sheet is electrically neutral (no net charge) and is carrying a steady uniform (magnetostatic) sheet current K = Kŷ in the y-direction. It may help conceptually to think of the sheet as having length L, width W, and small thickness d, as in the sketch below, with a uniform current denisty j=jŷ flowing through the cross-sectional area dW, so that K=jd. But we are interested in the limits that L and W get infinitely large, while d becomes infintestmally small.

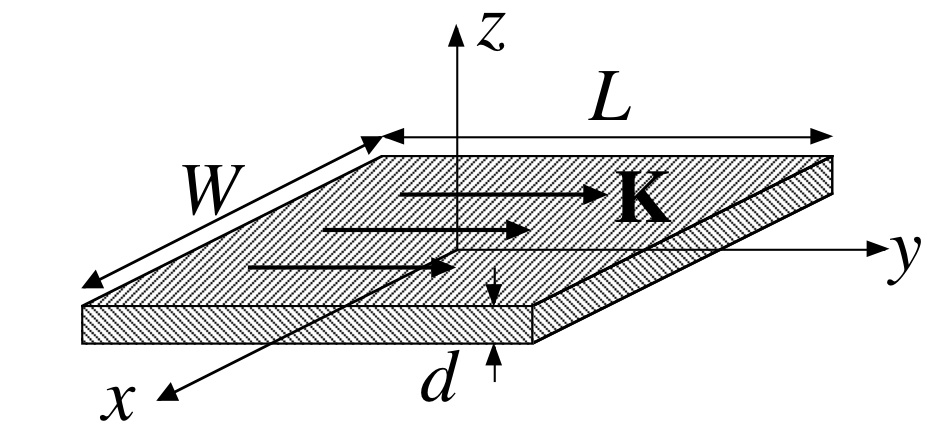
a) [3 pts] Find the electric and magnetic fields E and B for the above configuration.
b) [7 pts] Consider the above configuration as the inertial rest frame 𝒦 of the sheet. Consider now making a Lorentz transformation to an inertial frame 𝒦' that moves with velocity v=vŷ as seen by 𝒦. Using the Lorentz transformation for the electromagnetic fields, find the electric and magnetic fields E' and B' that are seen in frame 𝒦'? You should find that the magnetic field B' looks like that from a sheet current K', and the electric field E' looks like that from a surface charge density σ'. What are K' and σ' in terms of K and v?
c) [7 pts] Find the K' and σ' of part (b) directly by making a Lorentz transformation of the 4-current from 𝒦 to 𝒦'. Since the conducting sheet is neutral in frame 𝒦, can you give a physical explanation for the origin of the non-neutral charge density σ' in frame 𝒦' ? A simple explanation of the correct physics, rather than a calculation, is sufficient.
d) [3 pts] Is there a frame 𝒦' in which B' = 0? Explain your answer.