1. The Status at Our Last Meeting
2. Last Meeting's "Future Work"
3. Current Status
4. Current "Future Work"

Current Status

A More Robust Linear Solver Has Been Developed

Difficulty arises due to the nonlinearity in the diffusion coefficient—namely, its dependence on temperature. We may perform an integral transform on T to arrive at a form of the equation which does not have this feature.

The updated linear solver implements a new solver for an equation which has undergone a Kirchhoff transformation. The result is an equation which depends explicitly on transformed temperature (here, "θ") and implicitly on temperature T.

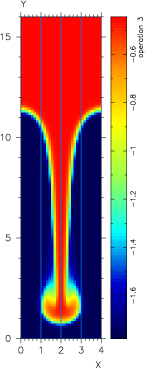
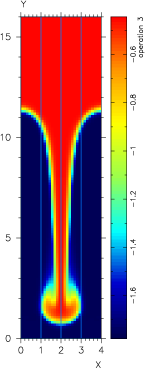
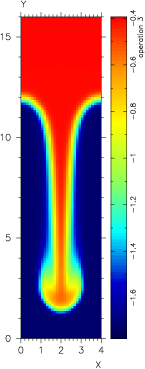
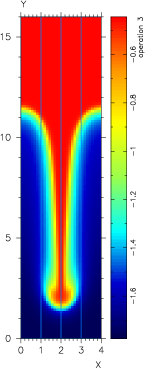
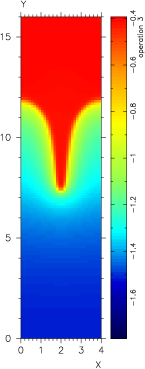
The addition of a solver for this transformed equation allows us to revisit the nonlinear cases which were beyond the scope of the solver prior. For our simple RT setup, the new solver is able to handle exponents on temperature from 0 to 2.5:

Varying: K*∇T, where K=k*Tω
No Linear Solve	Zero Coefficient	Constant Coefficient	Weakly Nonlinear	Strongly Nonlinear
	K = 0.0	K = 5d-4*T0	K = 5d-18*T	K = 5d-28*T2.5

Further Discussion is Required on the DT Ablator Problem

Here is a link to the page about the DT ablator.

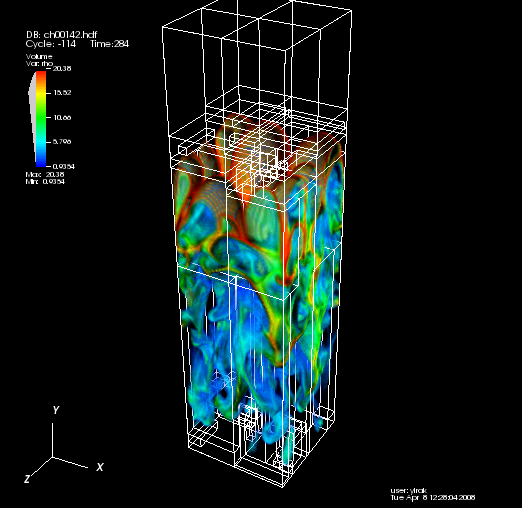
3D Multimode Classic RT Simulations Have Been Performed

The aforementioned difficulties were sorted out, and several runs have been successfully completed. Below is one example.

3d Multimode Classic RT:

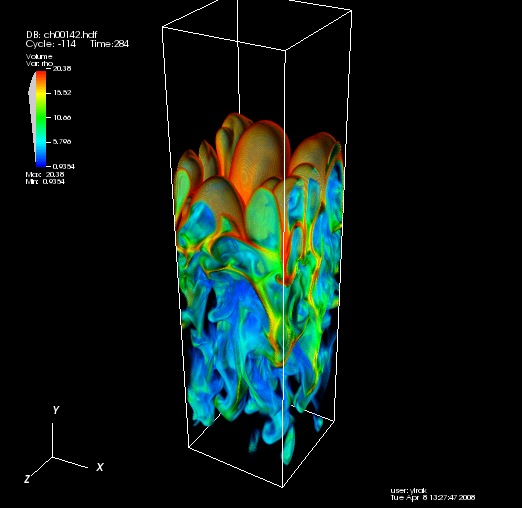
32x32x128+2 (128x128x512 effective) simulation seeding modes 4-8. Carried out on 8 processors, for roughly 10 days.

Here is the same simulation, with refinement regions overplotted: