mkal@mail.pas.rochester.edu
Homepage of world's smallest electric motor (quantum motor) and Quantum Electrical Engineering
While the Trojan electron does not stop and scatter and eternally moves with a constant speed
the
Drude time
time is infinite and the Trojan atom is
superconducting
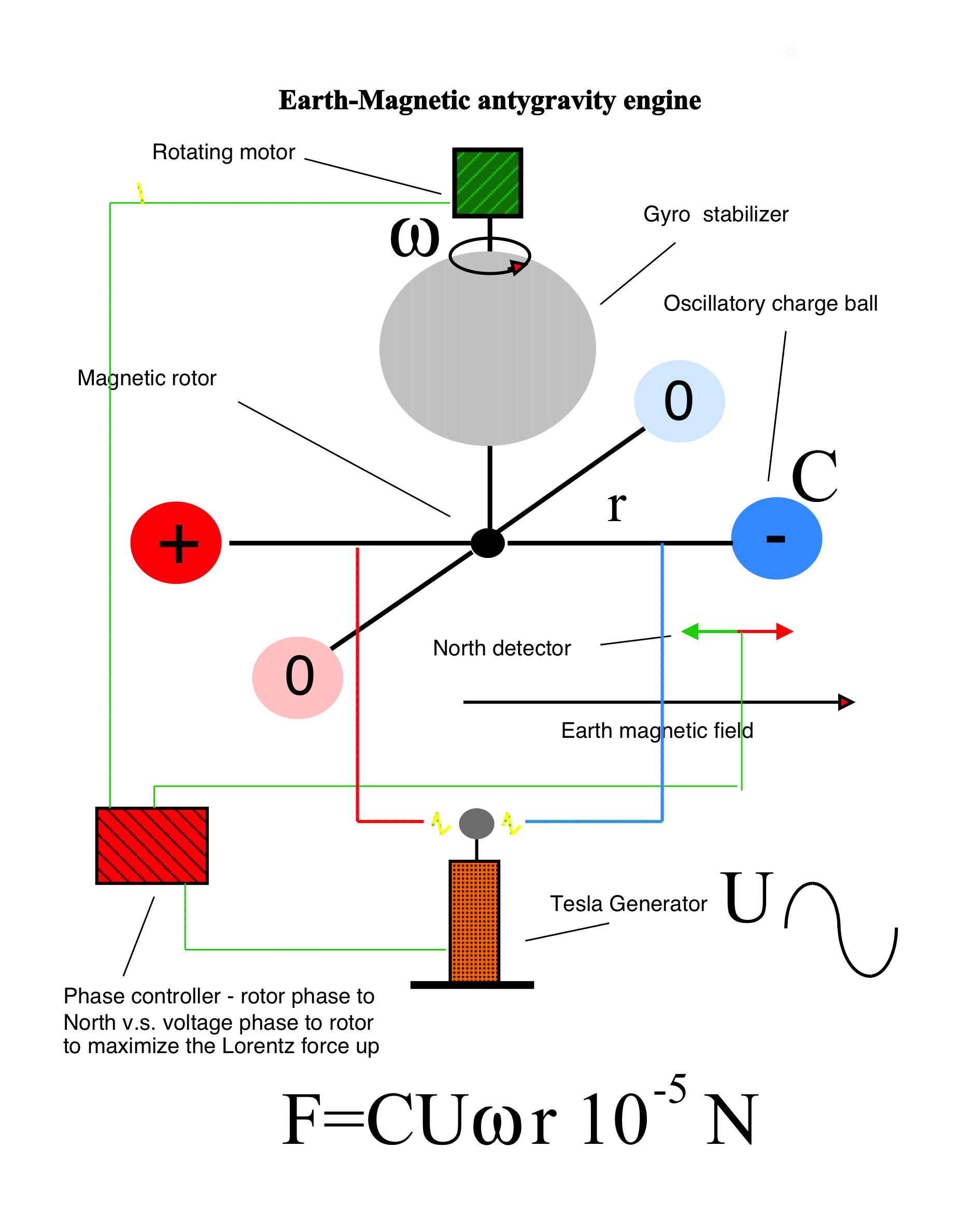
While the electron charge as small as 10^-19 C moves around the nucleus with the giant optical frequency 10^14 Hz the persistent current in a single Hydrogen atom is macroscopic 10^-5 A =0.01 mA and the Avogadro number of such atoms 10^24 holds the giant Meissner current of 10^19 A !!!
In the Earth magnetic field of 10^-4 Tesla the magnetic force extorded on such current if in a conductor with only 1 Angstrom lenght is 10^-4 x 10^-10 x 10^19 =10^5 Newtons or 10 tons of force and so in the magnetic field gradiend on a planet with the Earth value per this lenght or simply in the electromagnetic wave timed to the electron loop motion with the same magnetic field amplitude.
Photons seem to be a spin-1 particles with the Hamiltonian
being the projection of their spin and their momentum H = p S. Therefore
while hitting the objects inelastically they should transfer
their internal angular momentum and cause the rotation in analogy to
Einstein - de Haas effect .
Rigid black body disk will start to rotate under the influence
of the Circularly Polarized light (S_z= +-1). The smaller and the lighter the
object the better and the certain preexcited single electrons in atoms appear to be the best
candidates.
My research interests emerge from my PhD discovery at
University of Rochester
of
strongly localized
Starkstates for
Zeeman
Hamiltonian
so called
Trojan
states,
Landau states for electrodynamics with complex magnetic fields and mass tensor particles.
Trojan Wave Packets are the unique one per infinity Gaussian Rydberg-resonant Stark-Zeeman states of the Hydrogen atom in the
crossed electric and the magnetic fields when the Lorentz force is emulated by the identical Coriolis force by the Larmor frequency frame rotation but the diamagnetic harmonic interaction is balanced by exactly the same anty-harmonic from the centrifugal force and therefore there is no or the magnetic field is incomplete.
My PhD: The Hamiltonian of the hydrogen atom in the CP field is
H=p^2/2-1/r- e x - w Lz. When w=E2-E1 the matrix of it in the basis of two
first Hydrogen eigenstates of the type n=1, l=0, n=0 and
n=2, l=1, m=1 (only those two states are degenerate for the exact resonance in the
Bloch-Rabi
rotating frame for the perturbation theory
because of the Lz term) is H= {{E1, e d},{e d, E1}} with the
eigenstate |X1>=(|100> + |211>)/2^0.5 and the energy E(1)=E1+d e (Trojan wavepacket)
and |X2>=(|100> - |211>)/2^0.5 and E(2)=E1-d e (anty-Trojan wavepacket), d=128/243 a0. The first eigenstate is of the type 1 + Exp (i phi) while
the other 1 - Exp (i phi) for any fixed r. Therefore the first eigenstate
density is like cos(phi) localized around the angle phi=0 while the second is
Pi-shifted. The radial localization is due to the overlap between two
hydrogen states in r. Very clear banana-like shape of the packet can
be obtained in two-level approximation when one elevates the
excited n=2
component of the state by small detuning from the energy difference
so the relative radial contributions from both states are equal at overlap between a0 and 4a0.
One may therefore notice that the different energies of Trojan and anty-Trojan wave packet is also the
Autler-Townes splitting.
For the larger and larger n (w=E_(n+1)-E_n, l=m=n-1) wavepackets sharply focus relatively to the atom size as the 1/n effect.
In numerical experiments and without any analytical theory the hydrogen circular state simply behavies like it wants to touch you. When you tease it with the resonant CP field and the force against you it sharply polarizes into the opposite direction towards you.
While considered within the harmonic appoximation Trojan wavepacket ionization is equivalent to the
Dicke-Hepp-Lieb superradiant phase transition when the true collective field-matter electromagnetic
vacuum collapses and "Mexican hat" stabilizes in displaced state by the nonlinearity under the electromagnetic
interaction when the density of oscillator matter exeeds critical
While considered within the Mathieu theory and spanned by the circular eigenstates of Hydrogen it is a direct example of Poincare reccurence theorem in
a simple system when the full exact quantum revival and Poincare reccurence time of zero-field evolution after the creation became one for the interval being devisible by the all squares of the
quantum numbers in the expansion at once. Even for quantum numbers as low as 60 it becames hyperastronomical and therefore the Poincare time (10 to power 70 years).
When the relative dielectric susceptibility of matter X is -1 its relative dielectric constant epsilon = 1 + X is 0 (i.e. less than for the vacuum 1) and according
to the screened Coulomb law the infinitely small external field from the point charge will cause the infinite Coulomb 1/epilon r^2 force and
will induce the infinite internal electric field E=D/epsilon and the infinite opposite polarization causing it. Because of the NEGATIVE effective mass of the electron (anti-electricity in analogy to anti-gravity) this is the case of the Trojan matter. In practice because of the nonlinearity of response the polarization due to the infinitesimal
field will saturate to finite.
When considering the collective effects Trojan wave packets from their dipoles can generate together the internal electric field which consistently supports them so the external field does not need to be present. While the atomic dynamical response (Nonlinear unisotropic parallel resonant response theory of Hydrogen Circular States below ionization) and the polarizability of the Trojan state at the driving frequency is anomalous
and
negative (the dipole moment of the atom like a growing plant towards the light polarizes Trojan dipoles in the direction opposite to the electrostatic force from the capacitor plates charge surface density acting on the negative charge which normally orders dipoles to grow the capacitance) i.e. opposite
to that of the normal dielectric at static response and so their electric susceptibility X_0(omega_0) <0 and they are both nonlinear and strongly depend on the external electric field under the resonant distance conditions between Trojan atoms the gas can self-lock on nonlinearity without
any external field (While matching the outer empty space no normal field D=0 boundary condition for a Trojan electret stlab instantenously D = E - 4 Pi P(E) = 0 => E.ne.0, P(E).ne.0 i.e. the polarization is fully creating the internal electric field to cause it, above
the critical Trojan dipole density and P(E) is fast-increasing and strongly nonlinear with "transistor Ic vs. Vc" saturation) and the native state of interacting Trojan gas is dynamically ferroelectric (superconducting with ethernal intra-atomic Meissner-like sigle-electron persistent currents).
The two simplest three dimensional lattices supporting the native Trojan ferroelectric (and not anty-ferroelectric) order (all packets move in phase) on the microscopic Clausius-Mossotti cluster level (locked only on local field)
are primitive tetragonal lattice (direction stretched (here compressed) simple cubic lattice) and parallel hexagonal lattice - Trojan hydrogen atoms are on honeycomb
Graphene-like
two-dimensional lattices parallel to each other
and closer than the critical distance related to the intra-plane distances matching the atom positions projections perpendicularly and for both with packets move in planes. When the finite temperature is considered the temperature averaged quantum states being the thermal superposition of the circular Trojan manifold states
will under the Einstein B coefficient (de)-excite towards low dipole moment rotational states and therefore new kind of the superradiant first order phase transition occures (nuclear-like shape transition) from non-ferroelectric (circular states with zero polarization) to ferroelectric (Trojan states) state when the temperature changes and the dipoles become thermally insufficient. Because once localized by the field the dipole moment of the Trojan wave packet saturates
to its semiclassical value r_0 e (where r_0 is the Trojan Wavepacket orbit radius) and further almost does not depend
on the field electric i.e. self-consistently E = E_sc/r_0^2 = - P = N/V e r_0 = 1/a^3 e r_0 (where a is the distance
between the nearest Trojan atoms and Esc<0.11, a^3 is per-dipole volume)
the value of the critical parameter N/V e^2/m w^2 around 1 (omega is the main oscillator frequency i.e. the Kepler frequency of the packet)
remains the same that for the normal
ground-state Lieb superradiance superradiance which is also the same order (1/3 of that) when the susceptibility becomes infinite on singularity
due to the positive polarizaion feedback from the spherical dielectric hollow within the simple Clausius-Mossotti theory N/V e^2 / 3 m w^2 = 1 when the polarization centers are simple harmonic oscillators.
The Sinclair Basic code:
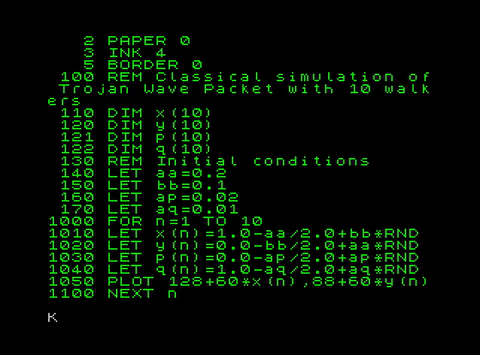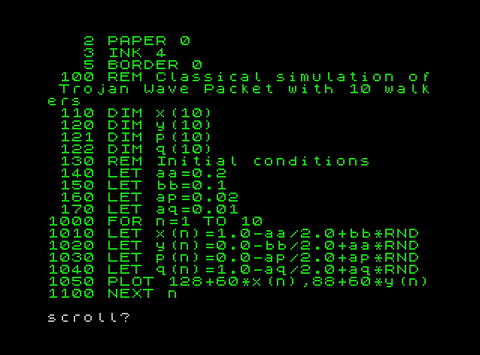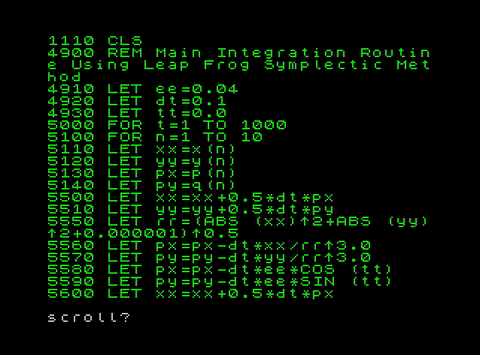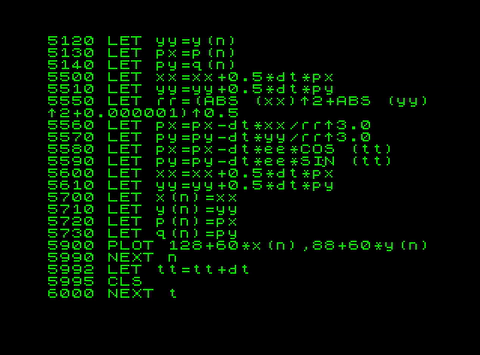
No CP field (spreading):
CP field ee=0.04 (non-spreading):
Simple man theory of Trojan wavepacket
Trojan wavepacket viewer
I
therefore engineered the smallest electric motor one can build with dynamic fields design
(with a single atom) !!!
In normal
electric motor (DC)
magnetic field changes around rotor adjusting
the torque to maximum for given phase (using the switch called commutator
)
In
inductive
or dynamic magnetic field electric motor (AC) the magnetic
field of the stator rotates around rotor with steady magnet (no commutator is nessesary)
In my motor the rotor is a displaced electric charge (dipole) not a magnet
(it is actually the electron on circular
Kepler
orbit)
and the electric
field is rotating instead of magnetic (the stator is the nucleus) -
you can also consider it as simplest example of electrostatic
propulsion on atomic scale
Like in classical macroscopic electric motor the bearing is not frictionless but the friction is with the electromagnetic vacuum modes - is radiative
Quantum motor while it works:
Mechanical model - electrostatic Coulomb force extords the torque
instead of magnetic forces - first designed by Physicists
Benjamin Franklin and Johann Christian Poggendorf
Trojan motor as circulating current has the magnetic moment and is subjected to forces in the magnetic field gradients amd therefore is a microscopic
Flying Gyro
experincing the magnetic antygravity
You can build a hybrid at home and power it with your TV screen !!!
or
Van de Graaff generator
(DC version)
I spent 6 hours tunning mine so be patient ... - focuse on bearing smootness (Marklin car bearing seems the best if you have time beyond ball pen bearing) and the sharpness of commutator needles (just needles)
(Or you can call it photon wind power plant if you like)
The tricky point is that with the quantum matter it is not so simple
- the rotor is really liquid and like a droplet of water exists only
within a fine parameter range (sizes of the droplet versus the electric
field strength).
(see the theory above).
The macroscopic applicable
electrostatic motor
whould have something
between the hard drive technology,
high voltage
capacitor technology and the
display technology - the volumetric multi-cylindrical capacitor
arrays in almost superfluid dielectric with thousands of electronically
switched sub-sectors and hundreds of sub-surfaces should be the best.
Old US patents of electrostatic motors
and now more complicated engine - Langumuir states
are physical in crossed fields !!!
APS
Making
Trojan wavepacket (or quantum motors) costs 500000 dollars but it generates
"visible" Hawking radiation in muonic Hydrogen
Since is accelerated with 10^25 g there
My free "ticking" symplectic solver for atomic clusters and astrophysics (forms Kepler "Cooper" pairs each time step) click the grey movie
to downoad, there is no Makefiles but you can alter it
This how the atoms get the kinetic energy during Coulomb explosion so the
cold fussion
occurs in
the Deuterium clusters micro-fog
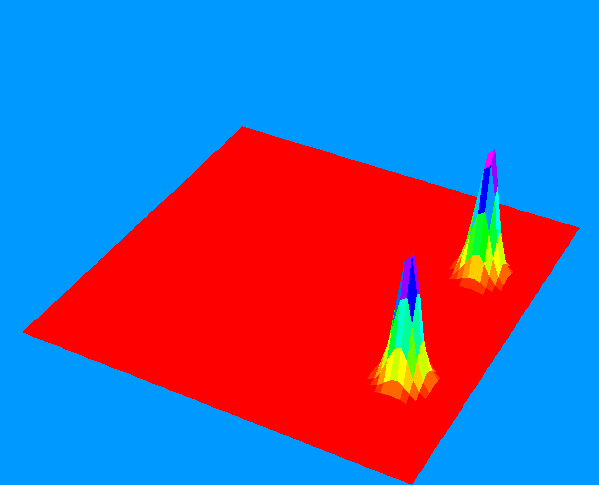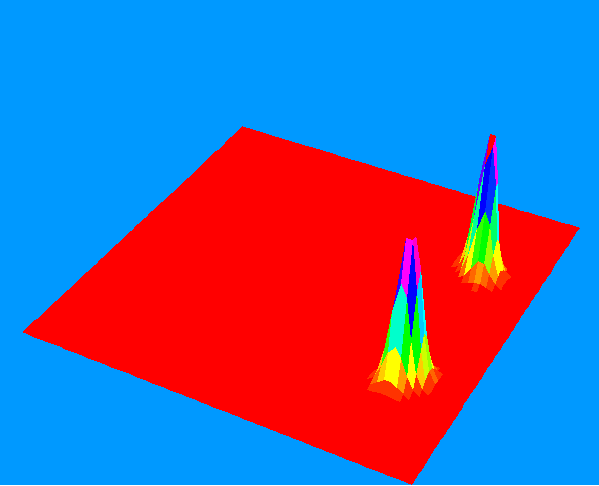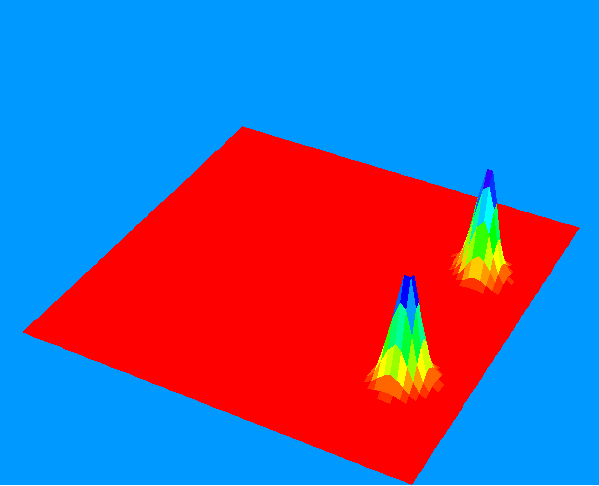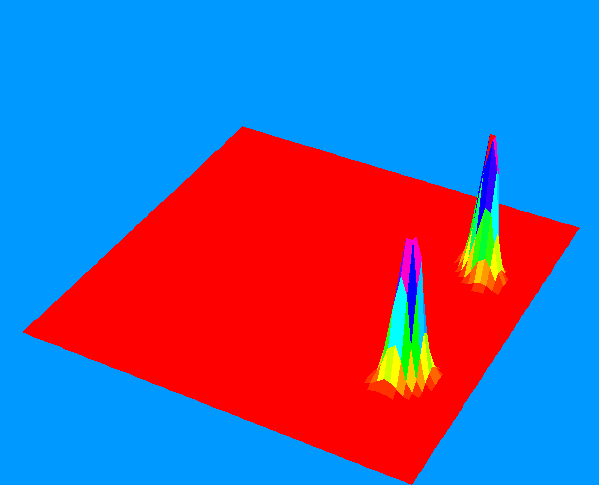
Two-electron pairs orbiting in strong magetic field (or electron-positron pairs in CP field). As the wave functions
do not overlap the recombination process can be frozen indefinitely
Other small and more or less quantum or electric motors
Proton powered rotating
γ subunit
Metal
droplet motors
Single molecule motor
with hydrogen-carbon chain rotor and sulfur-copper bearing powered by tunneling microscope
Molecular B13+ infrared ionic conductivity bicycle motor with chain powered
by the CP field with 13:1 derailleur in asymmetric Wankel configuration
Carbon nanotube bearing nanomotor powered by exchage of surface
electrons angular momentum
Various life inside-cell giant-molecular motors
Brownian motors - climbing with fluctuations
Carbon nanotube steam locomotive-like nanomotor powered by
temperature gradient
Like the model trains initailly localized wave packets will
move on periodic trajectories like on a track
spreading fast
on
unstable trajectories and not dispersing on locally stable
trajectories.
While all trajectories are points in a certain
instatenous rotating frame and the WKB wave functions spike
singularly around the turning points of zero velocity
there must be localized eignstates there around
to phase interfere.
The locally rotating frame augmented to the trajectory
tangent circle may be used to study adiabatic stability.
I am looking for various iteresting, for example 8-shaped trajectories
which can support on-average nonspreading Trojan-like wave packets.
Triangle, square and general polygon trajectories are possible
in atoms in combination magnetic and electromagnetic fields for one and more electrons.
Interested in selected exotic eigenstates,
I am currently working on Monte Carlo genetic algorithm implementation
of fixed node method. The nodal constrains are tossed randomly and
than the genetic operations are performed on best nodal populations
to produce better energy estimate of selected excited states and so on.
You can also use it with tossed-node imaginary-time split operator method
Studying the time dependent free dynamics of the Trojan wave packets after the sudden field turn-off I have
recently discovered that the full quantum revival occurs in any quantum
system with the rational energies and therefore asymptotically in near-ifininity in any quantum system.
Thus it is equivalent to the Poincare revival. While the normal revival considerations
expand the spectra up to be harmonic or quadratic as for the quantum well for the Trojan
wave packet the validity of expansion is equivalent to the expansion truncation.
Depending on the number of states involved in the time evolution expansion the exact revival time
of the Trojan wave packet becomes the Poincare when it is as long as non-physical on the Earth
laboratory time scale.
My hot topics for today:
Quantum theory of dielectric constant of organic materials
Inertial confinement of solid hydrogen
Theory of dielectric constant of Bose condensate
Superradiance
of Rydberg gases in quantum cavities
Car-Parinello simulations of egzotermic reactions
Cellular automata by quantum dots arrays
Physics of Magnetars
Fussion in atomic clusters in strong fields
Quantum monodromy in helium in crossed fields
Spontaneous light amplification through superradiant
emission of radiation (SLASER)
Non-fixed node Monte Carlo with genetic algorithm
Bose-Hubbart theory of color Bose and mixed gases
Nonlinear acoustic subsceptibilities of Bose Gases
Beta electron beams from on-wave acceleration
Detection of heavy mases with mesoscopic SQUIDs
Unruh-Davies effect from quantum entanglement
Ionization Kondo effect in Rydberg gases
Mesoscopic superconductivity
Split-operator methods for spinors and wave function of photon
in dielectric media
Contraction-of-propagator methods for protein folding
Quantum computing with quantum dots
Trojan wavepackets with Wannier excitons
Spontaneous order in systems with negative mass
Superradiance with mouonic hydrogen with cyclotronic motion
Spacial control of dielectric constant
Optical phase solvers of Schrodinger equations
Quantum entropy ordering with Trojan wavepackets
Ticking of quantum states
Quantum entropy fluctuations in systems with anomalous spectra
Chaotic oscillations of quantum states in rotating systems
Channeling in multi-center scattering
Model Born-Infeld theories with electromagnetic vacuum collapse
Bohm Hydrodynamical Quantum Mechanics and
real time Diffussion Monte Carlo
Dicke superradiant phase transition as supersolid formation in
Bose-Einstein condensate with oscillatory interactions:
uniform(normal) versus oscillatory (superradiant) phase
Cactoo fractals
Configuration existence theorem for N electrons in magnetic
and circularly polarized fields: The maximum number of configurations
may be the product of all differential foldings (maximum number of times
the ZVS gradient manifold is cut by a straight line
to the separate points):
There may be at least 2^180=1532495540865888858358347027150309183618739122183602176
maximum number of configurations of electrons corresponding to carbon
C60 (N=60) assuming the lowest nontrivial folding 2 (parabola-like).
The same applies to the molecules consisting of atoms if the binding forces can be assumed
to be conservative and have the potentials and their all components
have notrivial folding at least 2: There may be in principle 2^(3 N) distinct
molecules consisting of N atoms i.e. for example 2^180 allotropes of
the C60 buckyball molecules (like 3 x 20, 5 x 12 or 6 x 10 sheet of Graphene or 60-atoms
short Carbon nanotube etc.).
To see this theorem working in 3D one may consider a rose and two
planes as some differential ZVS gradient manifolds.
The rose has clearly high folding and then when cut again
perpendicularly is cuts to a lot of points.
In 4 dimensions the line can cut the perpendicular or non-containing
3D space at 1 point (the system of 4 linear equations - 3D space equation in 4D + the line equation has only one unique solution) and therefore the 4 dimensional ellipsoid a x^2 + b y^2 + c z^2 + d t^2 = e in 2 points
so there is maximum 2^4 = 16 solutions of the system of
nonlinear equations
consisting of 4 ellipsoid equations embadded 4 dimensional space or otherwise analytically
when such system of equations is linear for x^2, y^2, z^2, t^2 it has only one nontrivial solution for them and if they are all positive it has 2*2*2*2=16 solutions for (x,y,z,t) because of the double sign of the square roots of the former.
Concentration of primes: 469!-1 was once found prime and
469! - 1 -4362, 469! -1 -4902, 469! - 1 -5406, 469! -1 -5652, 469!-1-8580,
469! -1 + 1130, 469! - 1 + 2084, 469! - 1 + 2592,
469! - 1 + 6662, 469! -1 + 6998 are all prime !
11^1008 + 998672782 was once found prime and so IntegerPart[2(11^1008 + 9986727
82)^2 - 1)^0.5] + 3695 is.
Exact revival of the wave function of mathematical Hydrogen: The arbitrary wave function (not only
Gaussian wavepacket and approximately) will recover exactly for the system with the energies En=-R/n^2 after the
time T=2 Pi hbar Lm /R where Lm is the lowest common multiple of squares of all quantum numbers
involved in the wave function. When first 120 states are involved this is about 10^79 years !!!
Generation of
Langmuir Trojan states in Helium: First the Trojan wavepacket is generated
from one electron leaving He+ ion core, the plane of motion is adiabatically shifted by the
static Stark field turn on parallel to magnetic field and then
the second Trojan wavepacket from Helium He+ ion is generated but to
much smaller off resonant orbit not much to influence the first one.
Later "two color" CP field is adiabatically adjusted to one frequency
while turning off the asymmetric Stark and turning on the magnetic field.
Barnett-Einsten-de Hass (rotationally induced) quantum Hall effect: When Trojan wavepackets
are build from Wannier excitons and confined in quasi two dimensions the rotation of the
sample will induce alternating Hall voltage along the thickness due to normal ridid body rotator response in this direction. When the number of Trojan excitons is
quantized the Hall voltage will.
Detection of
gravitoelectromagnetic
F= v*dm/dt*(Gm^2/r)/(2 Pi m c^2)
Lorentz force with gravitational
Aharonov-Bohm oscillations in Trojan wavepackets.
For Trojan atom placed on the fast satellite orbiting Earth within about 1 hour in the
Trojan Michelson-Morley experiment the possible gravitoelectromagnetic
flux due to the Earth existence will shift the electron interference
pattern for n=600 by one full fringe during 1 year !!!
Trojan Hydrogen as Josephson Junction through
Quantum Phase Model (QPM)
"Compressed sping" phase transition
in Trojan elliptical harmonic
two-electronquantum dots
Coherent tunneling between two Trojan atoms in two ultrashort delta laser pulses
Trojan wave packets from electron gas in the Coulomb field of higly charged
ions in ultrastrong CP laser field
Uncertainty relations for excited Trojan wave packets
Exact revival of the wave function of arbitrary quantum system with rational energies. The quantum wave function
will recover exactly for the system with the energies En=C Nn/Mn
after the
time T=2 Pi hbar Lm /(C Ld) where Lm is the lowest common multiple of all denominators in fractions in energies
involved in the wave function and Ld the greatest common divisor of the numerators (most probably 1 for long sequences with large primes). Since the set of the rational numbers is so called dense in the set of real numbers
(for any irrational number there is the rational one arbitrary close to it) each
quantum system revives exacly on theoretical computer with truncated accurancy since any number there is integer/10^n.
Example 1)
Jaynes-Cummings Model:
Consider the energies of Jaynes-Cummings model En=(n-1/2)omega +- (1/2)[(omega-Omega)^2 + 4 g^2 n]^(1/2).
To make energies rational (integer here) let us assume the state is localized in n and spanned around the principal quantum number n0. The energy Taylor expansion around the leading state n0
is En= (n-1/2)omega + Const + g^2/[(omega-Omega)^2 + 4 g^2 n0]^(1/2)(n-n0). While the coefficient multiplying (n-n0) is small
we can assume omega is also the integer multiple of it. While only even or odd ns are involved (the eigenstates mix the consecutive photon numbers) we get the revival time (to revive the state up to the phase factor)
T= Pi*[(omega-Omega)^2 + 4 g^2 n0]^(1/2)/g^2
Example 2) Hydrogen atom for shorter times: Consider energies of hydrogen atom En=-1/2n^2. Let us assume that the quantum state is
localized around the principal quantum number n0
(Gaussian-like in n around n0) and expand En=-1/2n0^2 + 1/n0^3*(n-n0) -3/2n0^4*(n-n0)^2 to make it as varable integer multiplying the common rational.
Since the coefficient
multiplying the quadratic term is small to the Kepler frequency 1/n0^3, the Kepler frequency 1/n0^3 can be assumed the integer multiple of it.
Without the loss of generality we can assume expansion in n-n0 as even. Therefore the revival time is 2*Pi*n0^4/3.
Superrevivals in Jaynes-Cummings model: Mapping the revival dynamics of the Trojan wave packets after the sudden field turn-off onto the Jaynes-Cummings model the revivals in J-C models are
full rotations of the spreading Trojan wave packet while the full revivals of Trojan wavepacket are superrevivals in Jaynes-Cummings model after the time T= Pi*[(omega-Omega)^2 + 4 g^2 n0]^(3/2)/g^4
when the normal revivals will to reshape back to the original decay and around. The superrevival time is about n0/g^2 longer then the revival time !
Exact superfast revivals of special quantum states in Jaynes-Cummings model on resonance:
Let on resonance En =(n-1/2)omega + Const +- g n^(1/2) and omega is integer multiple of g
then any quantum state such that n = kn^2 revives exactly after the time Trev= 2*Pi/g when Trev* g* 2*Pi*n^(1/2) = 2*Pi*kn . Specifically the incomplete coherent states with the number state expansion holes and n components quantum numbers being the square will revive fast and exactly.
If kn are localized around large kn0 then kn^2 \approx kn0^2 + 2*k0*(kn-kn0) and n are approximately even or odd with the constant gap.
Looking for arbitrary primes using the exact revival of arbitrary quantum system with rational
energies: If En= C Nn/Mm (Nn=1, Mn=n^2 for Hydrogen) has Mn as the power of prime then the
superposition of N such consecutive levels has the autocorrelation
function always below 1 during the time 0 and the exact revival time 2 Pi hbar Mp1*Mp2...MpN/C
(lowest common multiple of primes is their product)
so if all first N of primes (really those up to MpN+1/2) is known
the next bigger N-th+1 can be found from no reaching 1 condition (or is MpN+1 a prime ?).
Phase shifted exact revivals of the wave function. Let En=C/n^2 and the wave fuction is the superposition of
such n that n=10^kn. Let knmax is the maksimum of kn in the wave function expansion. Lm=10^2 knmax and the exact
full revival occurs after time T=2 Pi Lm/C but since for the each integer 10^2 kmax/3, 10^2 kmax/3=3333...3 + 1/3
the phase shifted exact revival such that Psi(T)=Exp(i 2 Pi/3)Psi(0) happens already after the shorter time
T=2 Pi Lm /3/C.
Arbitrary state preparation with the exact revival of the wave function: Providing that the amplitudes
of the wave function are first prepared the arbitrary phases can be reached only by waiting for the sufficient
time of the quantum evolution as the time of the full revival with the energies renormalized
by the inverses of the rational phases up to full multiples of 2 Pi or the wave function phases sweep
the whole asymptotically infinitely dimensional phase hypercube modulo 2 Pi for the arbitrarily long time.
New method of Trojan Wavepacket generation: 1) Arbitrary Gaussian distribution of the circular states
is generated around the resonant state. 2) Free no-field evolution is allowed till the Trojan wave
packet is self-formed. 3) The parameter matching CP field is turned on instantaneously in phase.
Quantum gates with two Trojan atoms coupled by dipole-dipole interaction
with Trojan and anty-Trojan states as 0 or 1.
Dynamic ferroelectricity and antyferroelectricity in the system of interacting Trojan atoms.
Dirichlet problem for the d'Alembert wave equation with one periodically oscillating wall:
Let u(x,t) is the solution of the wave equation and u(0,t)=0 on one rigit wall at x=0 and further
u(q(t),t)=0 with q(t)=a+b*sin(w*t). Let f(x) = x + 2*a + 2*sin(w*(x+a)).
Then u(x,t)=g(f(f(f(...(t-x))))-g(f(f(f...(t+x)))) with the finite multiple Feigenbaum f composition
is slow on convergence to the fixed point or differs a little on the next interation and is the approximate solution when
g(x+2*a) = g(x) i.e. g is periodic with 2*a or exact for u(h(t),t)=0 with h(t) periodic and close to q(t).
Quantum scars
in infinite
stadium
potential well as
quantum carpets
for one-dimensional Klein-Gordon equation with the imaginary time
and time-dependent semi-circle boundaries u(q(t),t)=0 with q(t)=+-[a+b*$in(t/b)], $in(t)=[1-(1-t)^2]^0.5.
The scar energy is the square of the mass energy of the pseudo-relativistic
particle at rest.
The scar reflection from the parallel stadium edges is the
Klein paradox with the particle probality coming out from everywhere in the whole
volume (or the one-dimensional space) due to the imaginary time or
propagation velocity.
Kondo
temperature suppression of ionization of Trojan Hydrogen as
Superradiant
Phase Transition.
Trojan wave packet as the superradiant electron state of the Jaynes-Cummings model
after Holstein-Primakoff transformation for two levels
Quantum Hall effect and annihilation suppression in electron-positron gas
Cold fussion
of magnetically stabilized two-nuclei Trojan states of Deuterium
Slaloming of Trojan wave packet of Deuterium nucleus in Palladium
crystal lattice
Ionization probability dependent interractive
intelligent grid renormalization method for strong field
ionization problems # => []. Each time step the probability
to find an electron is calculated in the outer near-boundary spatial region. When
the critical is reached the size of the spacial grid step
is doubled and the wave function is rewritten from the previous grid
each second grid point being again far from boundaries.
Trojan stability paradigm in harmonic
two-electron quantum dots in electric and magnetic fields emulating rotation.
Soft chaos induced shape life of Trojan wave packets due to
Henon-Heiles
like corrections and randomness of "irrelevant" Stark-Zeeman energy levels.
Dynamic ferrolectricity of Trojan hydrogen atoms on 2D honeycomb lattice (Elok > 0).
Nonspreading wave packets of near-luminal electrons in free space.
According the relativistic energy-momentum relation E^2= p^2 c^2 + m0^2 c^4 the dispersion relations E(k)
for free electron and positron form the avoided crossing with the energy gap being twice the
rest mass energy of the electron m0 c^2 or the energy of the pair creation. As the result they become linear and photon-like in
utra-reltivistic limit k -> Infinity and Trojan-like wavepackets exist in free space moving with almost the speed of light.
They can be
generated
from Trojan wave packets (focuser) by ultra-strong phased electric field delta kick applied
to Trojan electron (accelerator).
Effective Hartree-Einstein equation for the relativistic electrons:
p^2/(grad S(x)^2/4 c^2 + 4 m0^2)^(1/2) + V(xt) + m0 c^2 = i d/dt, Psi(x) = |Psi(x)|exp[iS(x)]
Rotational "Third force" on Trojan wave packets:
In Electrodynamics there is other than the Coulomb Force and the Lorentz Force
force acting on particle without the electric charge but with the dipole magnetic moment
and with the spin (e.g. on neutrons) in the crossed combination of the electric and magnetic fields.
Because the free evolving spin with the magnetic moment undergoes the precession according to Bloch equations i.e. the end
of its vector axis moves around the circle and its tilt angle with respect to the magnetic field vector is constant it also generates the magnetic field
which is time dependent. This field is generating the magnetic flux which is variable in
time and according to the Faraday's induction law and the Special Theory of the Relativity it is seen
in the laboratory frame as the combination of two fields, the magnetic and the electric one.
Now if such spin is placed between the plates of the charged capacitor the variable in time magnetic flux from the dipole motion will induce
forces acting on rigidly mounted electric charges. According to the III Newton's principle of dynamics
about the reciprocity of force action this force also acts backwards with the same strength on the magnetic dipole. In the extreme condition of the precession
angle of 90 degrees this force is therefore in the direction perpendicular to the electric field and parallel to the magnetic field.
Such capacitor however is equivalent to the constant electric field generated by its charged plates.
In general case of the electric and magnetic field orientation the third force can be expressed as:
FIII=1/mc E x (m x B). The similar effect will be for Trojan wave packet when the electron spin is precessing under Eistein-de Haas-Barnett interaction in
the rotating frame.
Intrinsic Trojan-like i C x y
entanglement
in quantum systems and spin 1-space coordinateentanglement in the wave function
of photon
Violation of angular momentum Bell inequalities for two-atom entangled Trojan cat states
Electron free fall in the nuclear electric field and strong magnetic field: Trojan-like wave packets on
Gryzinski-like
trajectories in linearly polarized electromagnetic field with variable polarization plane.
Langmuir Trojan-like electron configurations on triangular, square and regular
polygon-
trajectories in strong magnetic and circularly polarized
fields
Direct determination of the vacuum impedance from the existence
of Trojan like wavepackets on regular poligon trajectories in the
magnetic field
High harmonic generation from Trojan-like electrons in strong magnetic field on polygon trajectories due to near-infinite vertex acceleration
Writing with the electron nondispersing wavepacket orbit in strong time dependent magnetic and electromagnetic fields
Detection of
Lense-Thirring effect with Trojan atoms:
Above the Earth poles the antygravity experienced by the Trojan atom with the the electron rotating in the
Earth spin direction is equall
to (2/5) n alpha^2*/(omega_Earth/omega_Bohr) g where omega_Earth is the 2*Pi(3600*24) Hz Earth rotation while
omega_Bohr is the first Bohr orbit frequency and while (omega_Earth/omega_Bohr) is measurable it is readily
measurable for ultra-Rydberg atoms with n = 1/alpha^2 = 137^2.
Cavendishexperiment for sigle atoms: Single electron cat states in the Hydrogen Rydberg pseudo-molecule to detect electron-proton gravity through gravitational Stark effect on Trojan wave packet
Delta pulse ionization current field effect single atom transistor (FET) using Trojan-anty Trojan dynamics
Direct exact violation of the
Second Law of Theromdynamics
by the spontaneous lowering of the
quantum vom Neumann entropy
in the ultra-long field-free time evolution of Trojan wave packets
Internal coordinate exitations of Trojan wave packet as the
Hawking radiation
Attosecond Transient Absorption by Trojan Wave Packets
Intensity dependent dielectric constant theory of incoherent Trojan wave packets: Assuming the Gaussian density
operator around the central state within the Trojan energy manifold of circular states the energy balance between the C.P. field absorption and the spontaneous emission predicts the existence of the
ethernal localized density Trojan wave packets in the decohering thermal reservoir even when the off diagonal elements of the density matrix are zero.
Microwave superconductivity of Trojan electron-positron pairs at finite temperatures
Trojan Positronium formation during electron-positron Bhabha scattering in the laser field:
The first step towards the Trojan matter-antymatter production is non-recombinating positronium in the Trojan wave packet state. In the first experiment
the
cathode
positron
anode
ray tube providing low energetic beams of electrons from cathode and positrons from anode covered by the positrons producing
radionuclide
are aligned to collide in the center between te cathode and the anode. While the collision point is subjected to the microwave or the laser circularly polarized field
finely tuned to the beam velocities and lepton beam densities
the Trojan
positronium
formation should occure to stop the matter and antymatter currents to pass through the collision point and reduce the annihilation and the gamma radiation.
Kronig-Penney (K-P) model
of supersolid formation with insulated delta potential: While the singular delta attractive interaction is added to the rectangular
potential barriers and both are taken as the interaction potential the Gaussian solitons formed because of the delta attraction while trying to tunnel organize in periodic structures to form supersolid in a weak external harmonic envelope potential: Stationary Gaussian solitons droplets form because of the locally solitonic Gross-Pitaevskii equation, they repel with the K-P potential while
are bound by the Bether-Peiers-Weiss potential from neighbours.
Hand writting with Landau states:
Because there is a symmetric gauge A = (-B/2 y, B/2 x , 0) in which the potential of the quantum particle in the magnetic field is symmetrically harmonic with the diamagnetic term with
the oscillator frequency proportional to the field it is possible to drive the Gaussian
Landau state
along the arbitrary
trajectory using the exernal potentials (time-split the propagator as Landau and the external potential). First the paramagnetic omega_c/2 L_z term may be eliminated by the equaivalent counter-rotation of the coordinate system and
the new time-rotated trajectory is the arbitrary for the Ehrenfest inverse dynamics problem for the ordinary potential for the Gausian packet.
It is why
the extra strong magnetic field is
improving the spatial confinement of Trojan
Wave Packet by x-reverting the stable rotating saddle point into the potential diamagnetic minimum and making it more orbiting Gaussian Landau state than the Trojan Wave Packet itself.
In two dimensions because the quantum and the classical time evolution equation for the Wigner function (i.e. clasically the Liouville phase space distribution)
is identical for the harmonic oscillator
which as quantum can only have piecewise negative Wigner functions Trojan Wavepacket is stabilized to exist for arbitrary low resonant quantum number by the
pendular
quantum nonlinearity
and Trojan-like wave packets exist without the nuclear hydrogen Coulomb field as simply
C.P. field accelerated Gaussian Landau states when one turnes-off the field of the hydrogen nucleus.
It is possible to find the time dependent CP field such that arbitrary trajectory
including hand written messages can be achieved in time first found by the inverse problem. While the changable width of the
Gaussian is pemitted the time dependent magnetic field may be also used in combination. Some kind of trasverse confining
potentials like the grid of Coulomb potential exends the method to three dimensions.
Weak excitations of uniform Gross-Pitaevskii condensate with ultra strong
self-focusing interaction
Stability of true quantum cubical atom
of Oxygen
in electromagnetic fields. While the exact static cubical atom with no fields in the vacuum is
the ion with only the fractional nuclear charge Z=(1+3*3^0.5+6^0.5/2)/2=2.4676... (end always unstable according to
Ernshaw´s theorem
the physical integer nuclear
charge maybe tuned either by the symmetric screening with the
dielectric constant cubic inner zone (precise - not Menger
Sierpinski sponge
(fractal dimension Log(26)/Log(3)=2.96565... > Log(20)/log(3)=2.72683... )
1-st interation (by removing (altering the dielectric constatnt in) only the central cube in lower partition)) or by the spherical harmonic quantum dot potential.
Collective"Hydrino"
flakes:
Storing chemical energy in Honeycomb self-sustained Trojan Atom clusters (Hydren) approximately
13.6 eV per excited Trojan atom (N*13.6 eV per N Trojan Hydrogen atoms)
Trojan wave packets in the quantum cavity as the ethernal, non-collapse and no-revival electron-photon superpositions immune to the spontaneous emission: Jaynes-Cummings-like model for the
infinite number of slightly off-resonant quantum levels: Our Mathieu theory can be extended to the full electron-photon system with the quantum electromagnetic field. The states with the fixed deviation of
circularity may be multiplied with the Fock states with the fixed number of photons and the augmented polarization in reversed quantum number order providing the proper
Jaynes-Cummings ladder energy exchange conditions. The
collective pendula in the electron-photon space are immune to spontaneous emission. Collective electron-photon Trojan wave packets with
the discrete level of confinement as the new quantum number dependent on the photon-electron ladder offset in such space are fully ethernal and immune to the radiative
decay and are the single electron Meissner effect for the photonic superconductivity.
While the circular energy states interact with the resonant modes of the cylindrical cavity the harmonization of total Jaynes-Cummings spectrum occures.
The field-electron superposition is the collective Schroedinger-Lorentz coherent Brown state for the Hydrogen-cavity with the non-spreading electron density and without the electromagmetic decay as only the phases of the circular states evolve but not the populations.
While the dressed pendular states are stationary in the laboratory frame the coherent superpositions of states with the different photon number
offset (for example with the coeeficients of the corresponding photon coherent states) with respect to the circular state running quantum number and with energes that now differ exacly
by the harmonic hbar omega are nondispersing electron density wave packets.
While they are photon-electron collective they are ethernal also
with respect to the spontaneous emission.
New method of no transient absorption spectroscopy detection of Trojan wave packet is implied with Positronium Trojan atom:
Positronium Trojan atoms in presumably Trojan state are injected to quantum cavity with compatibile quantum
C.P. field to maintain them in the Trojan states indefinitely. While the cavity has finite Q the Klystron power injection
is nessesary. After Klystron power turn off the enhanced gamma emission from the recombination should be observed while the positronium was
Trojan.
Ionization lifetimes of Trojan Wave Packets with hypergeometric-coordinate method appplied to normal circular or spherical
coordinates as the high angular momentum Stark states. The absolute scaled critical field is approximately 1/3.
"Recursion formula" (theorem) to construct arbitrarily large primes: Let N be the
primorial
of the prime k (denoted by the following #)
N = k# i.e. the product of all primes not larger than the prime k,
then there is such integer s (also may be negatives and sometimes larger then 10) that N - 1 + s*10^l is prime, where l is the decimal length of N . For example 2*3*5*7*11*13*17*19*23*29*31*33*37*41*43 - 1 + 800000000000000000 = 431731123945110989 + 800000000000000000 is prime and there is such number s(=8) for arbitrary k(=43),
l(=17) or 2*3*5*7*11*13*17*19*23*29*31*33*37*41*43*47 - 1+ 200000000000000000000 = 202913628254202165299 + 200000000000000000000 is prime k=47, s=2, k=20. It is Fermat-like theorem that the sum of N - 1 plus some existing multiple of its decimal length 10 power is prime.
The first candidates are therefore k s near the exponent of 2 (e) in the
largest known primes.
While N can be arbitrary large by induction theorem it proves again there is no the largest prime.
For example
29*10^15 - 1, 2*10^27 - 1, 6*10^28 - 1, 9*10^29 - 1, 48*10^30 - 1, 8*10^31 - 1, 21*10^32 - 1, 5*10^33 - 1,
6*10^34 - 1, 44*10^35 - 1, 11*10^36 - 1, 11*10^37 - 1, 15*10^38 - 1, 18*10^39 - 1,
6*10^40 - 1,
33*10^41 - 1, 30*10^42 - 1, 77*10^43 - 1
6*10^61 - 1, 6*10^73 - 1 are primes alone but 109# + 23*10^45-1 and
179# + 11*10^70 -1 = 139819592777931214269172453467810429868925511217482600306406141434158089, 181# + 60*10^72 -1 = 65397346292805549782720214077673687806275517530364350655459511599582614289
are primes.
Similar case: Localization of primes near the decimal powers: (large primorial is replaced by the small even number)
While the number 10 is only devisable by the primes 2 or 5 and so the 10^n it seems very unlikely that 10^n + s for small s (too small to be devisable by anything large) is devidable by
many primes while is close to 10^n and s is not devidable by 5 or 2 so must be sometimes only by one and be the prime.
So for the arbitrary n there is always a small number s with number of digits much less than
10^n (of the order of n in value) such that 10^n + s is prime: For example 10^123 + 3 is prime, 10^127 + 283, 10^1000 + 453, 10^1001 + 9337, 10^1002 + 1383, 10^1003 + 69,
10^1004+613, 10^1013+777, 10^1103 + 1693, 10^1203 + 597, 10^1303 + 729, 10^2000 + 4561, 10^3000 + 1027, 10^4000 + 16483, 10^5000+ 12123, 10^6000 + 9873, 10^7000 + 4981, 10^8000 + 5079 are primes.
Further there is always such s that 10^n + s is the prime and the s is the prime.
For example while 7 is the prime directly by the construction 10^100 000 000 + 7 may be the current
250 000 $ winning prime.
While the Mersenne number i.e of the form 2^n-1 has always the binary form 1111111.....111111
while 1 adds up to it to form that with one 1 and all zeros
and n is its number of digigs while this number of digits is devisable by some number it is
devisable by a shorter Mersenne number 111111 and the result is 1000001000001....1000001
By the binary multiplication that logically NAND-adds 1 from the left-shifted repetitions and AND-transfers 1 to th next column the length
n is then devisable by the shorter Marsenne number binary length tha can be any. Therefore n must be the prime for 2^n -1
to be a prime.
From the binary form form it is also the sum of the geometric series 1 + 2 + 2^2 + 2^3 + 2^(n-1) =
(1-2^n)/(1-2). Therefore by the same argument in any base system and the numbers looking the same i.e.
in the form 111111............11111
(1-k^n)/(1-k) may be good
prime if n is the prime. For example in decimal (10^19-1)/9 = 1111111111111111111 and (10^23-1)/9 =
11111111111111111111111 are primes while from the form in the base 5 (5^47-1)/4 =
177635683940025046467781066894531, in the base 6 (6^71-1)/5 = 3546245297457217493590449191748546458005595187661976371 and in base 7 (7^13-1)/6 = 16148168401 is prime while in base 11 (11^73 -1)/10 = 1051153199500053598403188407217590190707671147285551702341089650185945215953 is prime.
Lucas-Lehmer primality test
of Mersenne number using Trojan wave packet evolution after turn-off: Let M = 2^n - 1 is the
Mersenne number to be checked if it is a prime and Lm is the lowest common multiple of squares of all of the quantum numbers
of the states spanning the Trojan wave packet. Let us monitor the Trojan wave packet free (no-field) evolution at times
proportional to Lm*s_n/M when s_n is the sequence such that s_0 = 4 and s_n=s_{n-1}^2 - 2 then M is the prime (if and only if)
when the autocorrelation function < Psi(0)|Psi(t)>=1 for t = 2*Pi hbar/ R*Lm *s_{n-2}/M.
2^94897643-1 may be the largest Mersenne prime known. It takes about 100 days to check it up with Mathematica with the following code on
multi-GHz processor: M=2^94897643-1; s=4; Do[temp = PrintTemporary[n]; s = Mod[s*s - 2, M];
NotebookDelete[temp], {n, 1, 94897643 - 2}]; Print[Mod[s, M]] (when the last s Mod[s, M] is 0 M is prime)
Breathing chains of self-sustained Trojan Hydrogen in Quantum Gear modes: When two hydrogen atoms are in the trojan state in the same plane
at the on-line point between them they generate together the elliptically polarized electric field
with the polarization ellipse with 2:1 axis ratio but with the main circular component opposite to their dipole rotation. Therefore the neighboring wave packets will self-consistently counter-rotate while breathing in shape.
Noninterating entanglement
between two far Trojan atoms pairwise close to and interacting with others two: Let
two very far atoms almost non-interating via dipole-dipole interation be in the entangled Trojan state, for example in entangled Trojan cat
state: clockwise Trojan wave packet on one atom A times anti-clockwise on the other B plus the opposite |TA+> ox |TB-> + |TA-> ox |TB+>
+ terms to enforce fermion anti-symmetry
(anti-symmetric
entangled Hartree-Fock state). If now
each of the atoms interacts with close Trojan atom (there are two far H2 semi-molecules) via
the dipole-dipole interaction (There is totally 4 atoms)
the level of entaglemnt between far Trojan atoms will change despite there is no interation between them but only they interact with
close others (The close atoms perform semi-EPR measurement on the other by the dipole interaction).
Henon-Heiles
dynamics and chaos suppression near Trojan equillibrium point: The nonlinear Hamiltonian for Trojan wave packet
up to third order is H = px^2/2 + py^2/2 + a x^2/2 + b y^2/2 - (xpy-ypx) + c (x^3 - 3/2 y^2 x), with c approximately 1/N^2 a, b,
and thereforeHenon-Heiles-like type and full of soft chaos but quantum forces surpress it even when the wave packet covers
large regions of the classical phase-space for low quantum numbers N of the central component state.
Trojan wave packet generation from resonant circular states by sudden CP field rectangular turn-on/off, free sweep of quantum phase
hypercube till space localization and suddent matching turn on of the supporting CP field: The new method of the Trojan wave
packet generation seems to be possible in addition to adiabatic-rapid method to generate it from the circular resonant Rydberg state
using quantum energy rails Zener switches.
The suddent (growing much faster than the Kepler period) CP field turn-on projects
the circular state onto the highest Trojan states manifold consisting mainly of the
circular states with a different n number to superpose all the states. The circular state becomes the superposition of the angularly excited Trojan states freely evolving according to the phases proportional in time to the Trojan pendular energies meaning
that the circular states populations themselves change in time. The field is than turn off abruptly to maximize the circularstates population
closely matching the populations of the Trojan wave packet neglecting the phases. The spacially focused packet is rephased
during the free no-CP field Rydberg evolution sweeping the quantum phases hypercube modulo 2Pi and the matching
CP field is turned-on abruptly at the proper position phase
to maintain it.
Quantum Mechanics as the Diffussion with Transmutation: A new Time Dependent Quantum Monte Carlo Method is possible: Two kind of diffussing particles are considered which can transmute one into the other.
Each of the species undergoes the hyphotetical Einstein random walk progression with transmutation. The
progressed particles transmute into the particles of the other king before contributing to or annihilating the other particles density. This fully emulates the Time Dependent Schrödinger equation for any number of quantum particles. The negative sign of the real and the imaginary parts of the wave function is handled by the "spinor" densities carrying the sign as the degree of freedom. The walkers densities are substructed by defining the critical distance of nearest neighbours epsilon within which the substructed walkers annihilate each other like the antyparticles or are removing (capturing) each other from the board like in the game of Chequers and even change sign if the other walker space islocally empty within epsilon.
Kosterlitz-Thouless motion phase dynamic phase transition in Trojan Wave Packetsas rotors system on
regular lattices
Trojan Wave Packetsas
artificial time-optical lattice(Amost)-Quantum Time Crystals
Quantum Time Crystals are defined as "alive" ground states in which the internal motion cannot be stopped even
in the absolute zero like the persistent current is the superconductor so there is spontaneous periodicity and therefore crystalization in time. Because the following simple theorem holds that: for abritrary positive numbers a_i adding to 1 i.e Sum a_i = 1 the sum Sum a_i E_i (the Hamiltonian expectation in superposition) is always larger than E_0
if E_i are ordered growing the time dependent solutions with the energy lower then the ground state are not possible
for linear Schrödingers equation with the lowest eigenstate. It is however not immediately clear for the time-dependent nonlinear equations.
But those are also very difficult to imagine since only moving exact many-body states (superpositions) build from the full space eigenstates could lead to
moving mean fields through the density functionals but those would have to have also higher energy above the ground state because of the theorem.
For the quantum rotor in the magnetic field 2*alpha with the Hamiltonian - hbar^2/2 m r0^2 d^2/d phi^2 + alpha (hbar/i) d/dphi + m*r0^2*alpha^2/2
two-soliton-like solution (two bumps in density rotating with Larmor (half of the cyclotron) frequency) exists as e^-i*E*t Cos(phi-alpha*t) with the "kinetic" energy E=hbar^2/2 m r0^2 + m*r0^2*alpha^2/2 arbitrarily close by hbar^2/2 m r0^2 (the best condition hbar^2/2 m r0^2 = hbar alpha = 1 quant of Larmor which may be made as (negligibly) small as possible in temperature kT but still large (acoustic) in frequency
7.637 nK/kHz
to the constant ground state 1 (trivial in shape) as m or r0 grows to infinity. It therefore seems that it may generate similar solutions with the non-linear self-interaction but with the energy below the ground state. Similar states can be immediately constructed from three consequitive circular states
i.e. from two without the cetral for two-bump states but they will lower energy in the magnetic field because of the effectively negative mass of radial electron. Similar states can be immediately constructed from three energy consecutive circular states
spanning the Trojan wave packets with the Kepler orbital frequency resonant to the central state i.e. from two without the central one for moving two-bump states (standing in the Kepler rotating frame) but they will indeed lower energy at first look to the central state in the magnetic field because of the effectively negative mass of radial electron (negative kinetic energy on motion which has formally no botton but which is really the Hydrogen ground state) and all is spanned around the excited states.
They for example
may be Gaussons (As mean-field it corresponds
to infinite series of N-body Psi+Psi+Psi+...PsiPsiPsi interactions but is easier to solve) put in the solid state
Born-Karman
boundary conditions in one dimension coupled to the
one dimensional scalar magnetic field alpha as alpha*p=alpha/i d/dx (in one dimension here the magnetic field and the potential is one). While the Gausson momentum may be only discrete due to the B-K
conditions and
cannot match the arbitrary magnetic field alpha precisely while it is descrete the Gausson center velocity (alpha-k) cannot match 0 for abitrary alpha, the Gausson center must move
at the lowest energy (as it stays steady in the comoving (rotating) frame canceling the rest (alpha-k) i d/dx term).
Similar states can be constructed from three energy consecutive circular states which constitute mostly to Trojan wave packets but because of the negtive mass they will lower the absolute energy in the magnetic field.
Similar states can be constructed from three energy consecutive circular states which constitute mostly to Trojan wave packets but because of the negtive mass they will lower the absolute energy in the magnetic field.
Even if they are disputed as true normal ground states with the lowest energy
to exist rigorously
(the self-consistent stationary Bloch e^i{alpha-k)x* u(x) function with the Bloch vector (alpha-k) clearly exists for the
above problem while log |u(x)|^2 stays consistently periodic
which in principle may have the lower energy
(the leading correction from the term (alpha-k)/i d/dx within the first order perturbation theory for example from
the tight-binding Bloch function structure (simply average in this state) is only -2 (k-alpha)^2 Cos L (k-alpha)) <Psi0(0)|Psi0(x-L)> where the last factor is the overlap between
infinite line shifted perfectly Gaussian Gaussons
with the energy lower then "free band" kinetic (alpha-k)^2/2 and even negative (below hbar omega0/2) for small (k-alpha) and it later grows above 0 but is very small because the overlap is exponential in -L for confined gausson and can only exeed formally the
kinetic for overlaps of the order 1 (very weak interaction) and (alpha-k) = Pi/L) and which periodic solitonic part is the solution and it can move on weak excitation
as the interference pattern when unfolded above L = 2 Pi while there is no fixed 0 - the "wrong" Bloch function will creep under extra flux turned-on abruptly
for which it would be the (ground) eigenstate otherwise but was for different) one may imagine interactios leading
to Gausson broadening (self-energy lowering e.g. for relativistic) with motion and
there are clearly infinitesimaly excited states which approximate them very well and will be excited by the infinitesemal temperature or fluctuating stray fields.
It is a matter of the energy difference between the moving Gausson which is approximately hbar omega0/2 + (k-alpha)^2/2 and even looks conduction Bloch-band-like
despite the state moving shape time-dependence (exact value on the infinite line) and the energy
of the Bloch function with the Bloch vector (k-alpha) (which on the closed boundaries can be found precisely only numerically) which periodic part is the solution which appears to be not significant since for the
symetric part it will be only from the broadening or narrowing Gaussian shape to the moving Gausson so both are semi-degenerated in energy.
Trojan wave packets are quite similar even if it is difficult to talk about their lowest energy but better about their best topological simplicity. Especially the Trojan Wave Packet
consisting of two levels in extreme, the ground state and the first exited state with l=1 will move
periodically in time even without the C.P. field and with the energy near the ground state which is
the direct equivalent of the Zeeman creeping of the periodic Gausson with momentum k0: alpha= alpha-k0 +k0, in the smallest (k0-alpha) (k0,alpha>0) Zeeman field acting on its components
on closed boundaries splitting the propagation operator ((E1-E0) -> (k0-alpha)). For the exited Trojan Wave Packet being the
pendular "ground state" in the sense of nodal simplicity (Trojan wave packet the the maximal energy state because of the negative mass)
the
time crystalization as exactly defined originally would be the small Trojan packet oscillations or even oscillations-modulated rotational motion around the electric field vector after the sudden small off-resonance
detuning 1/n^3-omega turn-on from the formal discrete Kepler resonance equivalent to the magnetic flux i.e. the attempt of the cirular motion in the pendular potential around the C.P. vector static in the rotating frame rather than the Trojan circular motion itself or simply magnetic field can be turned-on while the electric off or lowered on generated Trojan wave packets for high Rydberg states to generate similar motion relatively in the rotating frame on slowly spreading or width-oscillating wave packets.
Almost Quantum Time Crystals in the model nonlinear system with "Coulomb" potential in mean field modulus:
The nolinear Gausson-like Hamiltonian H = -(1/2) d^2/d phi^2 + (A/2) 1/|Psi| (Singular repulsive 1/|Psi| v.s. singular
a*Log|Psi|^2 leading to Gaussons) has the "Solitonic" (+1 elevated cosine looking Gaussian) solutions with the
periodic boundary condition Psi(phi) = Psi(phi + 2 Pi) Psi(phi) =A (1 + Cos(phi)). Those solutions have energy E=1/2.
When the system is put in the magnetic field alpha then H = (1/2) (1/i d/ d phi - alpha)^2 + A/2 1/ |Psi| and
the time dependent solution A (1 + Cos(phi-alpha*t)) has the energy only E = 1/2 + alpha^2/2 while the constant solution
Psi= (3/2) A (the same particles normalization) the energy E = alpha^2/2 + A/2 (2/3)^0.5. It can be higher than
for the time-dependent if A > (3/2)^0.5 The approximate static solution (without caring about closed boundaries for small alpha) A e^{-i alpha phi} (1 + Cos(Psi)) has still lower
energy 1/2 (exact for alpha = 1) but the nodally simplest eigenstate can have higher. The first order perturbation
theory with respect to 1/i alpha d/dphi (zero contribution from symmetry of the solution without it) gives on the other hand exactly the energy of the moving state 1/2 + alpha^2/2.
Quantum Mechanics as the perturbation to Classical Mechanics: The nonlinear Schrödinger equation proposed by Shay propagates the wave function which is exactly equivalent to the density of walkers moving according to the Newtonian equations and with the velocities contained it the gradient of its phase. Therefore the exact quantum Schrödinger equation can be considered as the perturbed to the Shay equation. The time-dependent perturbation calculus can be performed with respect to the quantum potential back added while it is expressed is some scaled coordinates in which it is small (1/N)(for example N=omega^-(1/3) where omega is the characteristic frequency of the quantum system) correction and the zero quantum perturbation wave function is reconstructed from the purely classical simulations of the ensamble.
Inverse classical harmonic generation problem for the one dimensional potential: The time dependent solution for the motion of the classical charged
particle is assumed as the high terms desired Fourier series expansion up to the very high term enforcing the n-th harmonic. The external harmonic force is
added to the classical uknown potential to produce the proposed highly anharmonic solution. The potential is Taylor expanded also to the very high power of the space
coordinate (time dependent polarization). While the high powers of the proposed Fourier series are calculated the terms multiplying the n-th order Fourier oscillatory terms
are collected containing also the potential Taylor series coefficients as uknowns which can further be obtained from the resulting linear system of equations to reconstruct the desired potential. The problem effectively reduces to finding the desired trunaction of the n-th power of the time Fourier series in the Exp[i n omega t] which may me obtained by the recursive tensor multiplication of the vector of the lenght N by the another vector of the same length to costruct the NxN matrix containg the all products of the original vectors elements and then the summation of all anty-diagonals of the the smaller submatrices of the
resulting product matrix with the common left upper corner to contruct the next vector to multiply it by the original till the desired power is obtained.
The nonlinear quantum mechanics of Shay with the Schrödinger equation - d^2/2 d x^2 + V(x) + d^2/d x^2 rho^0.5/2 rho^0.5 = i d/dt (rho = |Psi|^2) immedialy predicts the approximate short time solutions with a
stationary density but with the internal motion: Let the wave function Phi was real at the t=0
i.e. Phi=rho^0.5. Then assuming it did no become significantly complex during the initial evolution
the kinetic energy term cancels exacly with the action of the anti-quantum potential and the Shay Schrödinger equation simplifies to V(x) = i d/ dt. Then the solution is Psi= rho^0.5 e^-i V(x)t and the
velocity field of Bohmian trajectories is vel(x)= - d/dx V(x) t which is a solution of the Newtons equation for short time
with the local acceleration field a(x) = - d/dt V(x). Therefore it appears long time solutions
are possible with the internal motion but the steady density.
For the harmonic oscillator the approximate solutions are possible in the form of the constant density eigenstates but full of the internal motion in the form Psi= e^-a*x^2/2 e^i*Integral(2(E - V(x))^0.5 (a is related to the turning point for the energy E as 1/x_turn^2 =a). Those states are full of the internal natural velocity field v(x)= (2(E-V(x))^0.5 with the Bohm trajectories obviously executing the harmonic oscillatory motion but not changing their density in time. In general there is no reason why this motion would not be chaotic but the desity still stationary.
Chaos drag and steady flows of Bohmian Trajectories within the Trojan states in Shay Quantum Mechanics:
The Bohm Trajectories for the Quantum mechanics of Shay are exactly the classical trajectories. The stable
shape invariant Trojan Wave Packets within the nonlinear Shay Quantum Mechanics therefore contain the steady
chaotic flows around the Lagrange equillibrium points leading to non-changing particle densities as the dynamics is
locally Henon-Heiles-like.
Chaos in Bohmian trajectories in quantum extended two-dimentional rotating continuous
Feigenbaum map
: It is known that the functional powers of the Feigenbaum (logistic) function f(x) = r x (1-x) f^n(x) = f(f(f(f(...(x)))) as higher and higer order polynomials change the number of solutions of the polynomial equation f^n(x) - x = 0 upon the change of the parameter r from the powers of 2 to infinity which leads to chaos of the interations trajectories x_n+1 = f(x_n). The discrete map can be readily extended to 2 dimensions as x_n+1 = f(y_n), y_n+1=f(x_n). One may rewrite it as
x_n+1 = f(y_n) - x_n + x_n, y_n+1 = f(x_n) - y_n + y_n or x_n+1 - x_n = f(y_n) - x_n, y_n+1 - y_n = f(x_n) - y_n. While mapping 1 -> dt the continuos version is dx/dt = f(y) - x, dy/dt = f(x) - y and the Newtonian (Hamilton) version
is d^2x/dt^2 = df/dy dy/dt - dx/dt, d^2/dt^2 = df/dx dx/dt - dy/dt. The Hamilton function can be contructed and quantized
assuming px = dx/dt, py = dy/dt. While the rotation is imposed by adding the term L_z = x py - y px the original Hamiltonian Bohmian trajectories of the eigenstates will exhibit chaotic behaviour.
Origin of classical chaos around the Trojan and anti-Trojan Lagrange equilibrium Point: When the Coulomb potential in the rotating frame which is the same Coulomb potential is expanded around the Trojan or anti-Trojan Lagrange equilibrium point till the forth order and the discrete
Euler integration method
is applied the resulting map resambles the two dimensional Feigenbaum map. Therefore the origin of chaos around that points is that of Feigenbaim. It is a result of the periodic alternating reflection from the line inclined at the 45 degree angle and the 90 degree refraction from the smooth polynomial curve which leads to the random distribution of the refraction and the reflection points upon exceeding the critical values by the curve coefficients.
Sligthly wiggling but a very good approximation for the error function Erf(x)=(2/Pi)*ArcTan((x*(2+x^4*2)) reversible to quintic equation solvable by Banach-Newton operator iteration gn(x)=(4*f1(x)^5 + f1(x))/(5*f1(x)^4 + 1), f1(x) = 0.5*Tan(x*Pi/2) and
another one reversible by Ferrari's formulas from quartic equation Erf(x)=Sign(x)*Tanh(|x|*1.152 + 0.064*|x|^4)
Einstein equations as the intrinsic property of the differentiable manifold: While the Lentz-Faraday induction law and the Maxwell-Faraday equation can be derived from the
existence of the (x) Lorentz force by a vector division of the induced electric-like force field and the magnetic field sweep and the coefficients of the
affine connection are forming the gravitomagetic field vector generating the gravitomagetic Lorentz force through the geodesics equation the Einstein equations appear to be
more the intrinsic geometric property of the manifold than externally imposed as the augmented gravity induction laws are therefore implied for the affine connection
and the components of the energy-momentum-stress tensor with the main Gauss law component are not independent.
Critical condition for the superradiant phase transition from the electrostatic and classical considerations only: consider the cubic lattice of the (locally) harmonic oscillators with a frequency omega with the lattice constant a and each filled with one electron. Consider one electron with 4 in-plane nearest neighbors which when assumed rigid create the anti-harmonic oscillator potential in the plane perpendicular direction. The 5-th central electron motion becomes unstable in the Coulomb field of 4 when the net harmonicity of the oscillator is negative i.e m omega^2/2 - 4 *e^2/ 4Pi /epsilon 0 (1/a^3) < 0 or e^2/Pi/epsilon 0 /m/omega^2 >1 . Making it artificially quantum by multiplying the fraction up and down by hbar we have e^2 hbar /Pi/epsilon 0/m/hbar/omega^2 > 1 or 2/Pi |D12|^2/E12/epsilon0 (N/V) >1 where |D12|^2 = e^2 hbar/2 m / omega is the transition strength between first two quantum harmonic oscillator levels, E12= hbar omega is the energy gap between them and (1/a^3) = N/V is the spatial 3D harmonic oscillator density. This is identical to this of the original superradiance by the Hepp and Lieb if the two levels are approximated by the harmonic oscillator (Holstein-Primakoff approximation).
Single atom Quantum Hall Effect with the Trojan Wavepacket. While the motion of the
Trojan Wave packet is a single electron current I =e/T = e f = e omega / 2Pi and defining the Hall Voltage as the Coulomb Voltage (the difference between the Coulomb potentials) (Coulomb force is acting as the Lorentz force balancing the centrifugal like for the free cyclotron motion) between the infinity and the point on the Trojan wave packet orbit U = e/2 Pi/Epsilon_0/r the sudden jumps of r as the function of omega taking the Bohr values r_n = n^2 a_0 for omega_n=1/n^3 (a_0 is the Bohr) radius lead to the quantization of the Hall resistance R=U/I around the jump points, R_n=n (h/e^2) (here linear but not inverse in n).
Trojan Wave Packets above the classical stability threshold. While the anti-Trojan wave Packets exist as an approximate product of the
inverted pedulum state which means that the classical trajectories indeed fall and spill from the unstable radial maximum and a Gaussian circular state and are localized around the always ustable equillibrium point it appears that also
states of such type should localize around the Trojan Wave Packet equillibrium point when it is unstable above the critical field but when the rotational stabilization or the
destabilization of the saddle potential becomes insignificant to the electric field potential. Those will no longer have Gaussian radialfunctions but some of the Bessel J_0 like inverted pendulum type. The destruction of the Coulomb spectrum in the rotating frame is so strong that the Mathieu theory in the Hydrogen eignestates basis is no longer valid because of large energy coupling between the states.
Finding the perfect Trojan Wave Packets directly with the Power Method. The Power Method http://ergodic.ugr.es/cphys/LECCIONES/FORTRAN/power_method.pdf for the eigenvalue problem does not require the matrix storage to solve the eigenvalue equation. In the essential two space dimensions the method may be used for sparse Hamiltonian of the Hydrogen atom in the C.P. field in the finite difference approximation on either x-y grid or r-phi (r - angular momentu m) grid. Each recursion of the for example Psi(x_i, y_j) 512 x 512 numerical vector is equivalent the time dependent numerical integration of the Schrödingers equation using the FFT method i.e. one integration for one consequitive eigenvector to project it out for the next dominant eigenvalue.
Cold fusion in the Trojan dynamic ferroelectric clusters: While the regular ultra-cold 2D lattices (flakes) consisting of the Hydrogen atoms in the Trojan wave packet states
coupled to each other the volumetric dynamic ferroelectric is possible due to the dipole-dipole interaction between the Trojan electrons. Each
atom while highly excited to the Trojan state carries approximately 13.6 eV of the chemical energy. While such matter suddenly collapses due to the thermal decoherence to the hydrogenic ground state 13.6 eV
of the energy is released from each atom through radiation. When the Hydrogen is replaced by the Deuterium 4 keV of the fussion activation energy can be obtained
for the primary ignition from 300 atoms for one secondary fussion event and the further chain reaction.
Self-amplyfying high-energy solitonic phononic waves in the Deuterium sublattice of the fully packed Palladium Hydride as initially displaced phase-triggered system of
Coulomb-interacing quartic oscillators
Trojan Wave Packets in Helium atom in configuration space: While the 1D model of
the Helium atom is similar to 2D model of the Hydrogen atom and the hyper-linear polarized electromagnetic field has two counter-rotating hyper-Circularly Polarized components the semi-Trojan Wave Packets are possible in the configuration space of Helium in the linearly polarized electromagnetic field.
For the true physical 6D helium atom they correspond to highly correlated low angular momentum wave packet motions along the electromagnetic field linear polarization phased withfield when the electrons periodically avoid each other approaching the nucleus and later tunnel through each other.
Langmuir-Trojan wave packets on the oscillating Click-Clack electrons Helium
semi-circular trajectories:
The Hamiltonian of the two-electron Helium atom while the constraints are imposed on the electron position that they both move in plane and their distances r from the nucleus are equal and their angles to some line in the the plane are of the opposite sign i.e. their positions are symmtric with respect this line is H = p_phi^2/mr^2 + p_r^2/m - 4/r + 1/2^0.5r 1/(1+cos2 phi)^0.5 when phi is the angle of the one electron position. While expanding the mixed r and phi potential in cos 2 phi around 1 it becomes approximately the Hamiltonian of the pendulum with the angle 2 phi and the radial oscillator bound by centrifugal barrier of the near rotary pendulum motions. Therefore the click-clack semi-circular trajectories are possible as predicted by Langmuir in 1921. When put symmetrically in the linearly polarized along the line joining the bouncing points electromagnetic wave they will selectively couple to two counter rotating C.P. components of the L.P. field supporting oscillatory bouncing Trojan Wave Packets on half-circular orbits. Alternatively if the electron-electron interaction was approximated only by the hard ball interation and the electron-nucleus kept exact the temporarily corotating C.P. field componets couple to stabilize the half-circular motion between the perfect bouces to Lagrange equilibrium points in the temporarily co-rotating frames.
Convenient parametrization of the Langmuir Click-Clack Trajectories: The excited Langmuir trajectories of the type (2) i.e. those corresponding to the Click-Clack ball motion may be readily obtained by reversing of one of the velocities of the intuitive planar circular 2-electron trajectories when the centrifugal force acting on the one electron is balanced by the Coulomb force of the positive nucleus and the repulsive forces of the other electron i.e. of the radius r, m w^2 r = Z/r^2 - 1/(2r)^2 i.e. asking for the instantenuous initial balancing of such forces when the electron are collinear with the nucleus. The velocities leading to the circular trajectories are therefore (0,w r,0), (0,-w r,0) if the initial electron positions were (r,0,0), (-r,0,0). It takes 1.09 scale factor of the initial velocities to focuse the excite trajectories to perfect sharp Langmuir bounding when one of the initial velocities is reversed while keeping the initial positions for those of the circular trajectories.
Hopf bifurcation
around the Trojan Wave Packet: The transition from stable to unstable dynamics around the Trojan Wave Packet is
equivalent to Mexican hat superradiant phase transition while the higher order Hamiltonian corrections are considered and the Hopf transition
The supercritical Hopf phase transition in the dynamics occurs because the essential part of the effective 2D Hamiltonian ar^2 + br^4 changes the character
from the quadratic-quadratic minimum (a > 0, b > 0) with the trajectories circling around 0 or approaching 0 when the infinitesimal damping is added or
circling around or converging with infinitesimal damping to the radial minimum circle (the limit cycle attractor) of the Mexican hat potential (a < 0, b > 0) when the
harmonic stability of the equillibrium point changes from stable to unstable.
Trojan Wave Packets in kicked Hydrogen atom: The Coulomb-contracted Coulomb-Volkov split operator method in which the exact Coulomb quantum propagation is alternating with the infinite mass particle propagation in the C.P. electromagnetic field potential realizing exactly the Hydrogen atom kicked periodically
by the Dirac-Delta spikes
of the Circularly Polarized electromagnetic field suggests the existance of the Trojan-like wave packets in such exact non-infinitesimal situation.
Ionization of atoms in Sperically Polarized (S.P.) Electromagnetic field: Up to six phased perpedicular laser
beams which are pairwise parralel are capable to generate fully 3-dimentional time dependent electric fields in their
crossing spot to superpose into the two-frequency superposition with the constant electric field vector
lenght: E(t)=E0*[Cos(w1*t)*Sin(w2*t), Sin(w1*t)*Sin(w2*t), Cos(w2*t)]. While the electric field vector end trajectory
is "fully curve" (unlike for the C.P. field which is the circle in plane) i.e. the any tangent plane to it has exactly one common point with it new ionization
phenomena occure.
Trojan-like Wave Packets in Spherically Polarized (S.P.) Electromagnetic fields moving on Sperical Lissajous-like trajectories in the ultra-strong field limit: When the Sperically Polarized electromagnetic field is composed from the linearly polarized fields with frequencies incommesurable enough the free electron trajectory driven by it will densely sweep the surface of a sphere. Suc spherical trajectory in the Kramers-Hennberger frame when time-averaged will first be seen as the spherical Coulomb-like potential with the singularity at the sphere surface which can be approximated by the Delta function. Such potential has the radial maximum at the center leading to the inverted-pendulum localization i.e. highly localized Bessel-like function wavepackets
centered at that point. In the laboratory frame such packet will therefore quasi-randomely move around the surface of the free motion sphere on a Spherical Lissajous-like trajectories and will not spread being pinned by the sphere delta potential enforcing the boundary conditions.
Trojan Wave Packets within the first order perturbation theory for degenerate states: No matter what the approximation philosophy by the smallness
of the certain dipole matrix elements is the method of simplifying the
exact non-separable Stark-Zeeman Hamiltonian matrix into the block--diagonal
form described in the paper
[1]
is formally equivalent to that of the first order
perturbation calculus for the degenerate states
applied to the partial magnetic field (with diamagnetic term only) Zeeman Hamiltonian H_0 = p^2/2 - 1/r - omega L_z
(cyclotron frequency equal to 2 omega) with respect to the
Stark
rotating frame frozen C.P. electric field term
if the states with the fixed deviation from the circularity i.e with with a constant differences of the quantum
number l and m from n were degenerate in the rotating frame (those near the resonance i.e. around some Rydberg
energy where the distance to the next one is that of the C.P. field quantum) but they are only approximately
i.e. the secular eigenvalue equation for each (approximately) degenerate energy value is solved in the basis
of those states within each sector only keeping the diagonal exact as it was i.e including the small energy
splits into the full perturbation. It is only the later to notice that each such submatrix to be diagonalized
to remove the (approximate) degeneracy (which is the kinetic energy and the source of the negative mass) is
additionally approximately tridiagonal with a constant off diagonal values e E_0 r_0/2, r_0=n_0^2, omega=1/n_0^3
(while the problem is basically 2 dimensional the radial wavefunctions of circular states are residing in
the minimum of the net Coulomb and centrifugal barrier potential as ground states and are approximately
Gaussian and not very different for n and n+1 so the radial integral of the dipole matrix element of x = r Cos(phi)
is approximately r_0 while the angular between exponents is that of Cosine and three-diagonal i.e 1/2) i.e therefore
pendular which is only the approximation to the Schrödinger equation within each (approximately) degenerate manifold.
The Trojan Wave Packet is therefore the unique Stark-Zeeman state built from the manifold of the circular states
only and therefore Gaussian in three space coordinates. The algorithm of the perturbation calculus
may be therefore performed further
with
respect to states of formally removed approximate degeneracy to obtain the better approximation to the spectrum
and the Trojan Wave Packet. However while the perturbation calculus algorithm is done strictly assuming fist
that the negative mass rotor contribution has so small that a relatively constant energy the resulted Stark
perturbation matrix is exactly solvable Töplitz matrix
performed further
with
the off diagonals equal to e E r_0/2 and diagonal to 0 therefore the approximate pendular spectrum restoring
the original small degeneracy deviations within a fixed manifold is - 3 hbar^2 (k-N/2)^2 /(2 m r_0^2) k^2 + e E r_0 Cos(k Pi/N+1) k=1, ..., N
where N is some assumed as bound with the Trojan wave packet with the highest value e E r_0 and the anti-Trojan with the lowest - e E r_0
giving the Stark-(Zeeman) levels as functions of the field fan only qualitatively.
The approximate form of the circular states as radial Gaussians around the Bohr
radius with the angular phase spanning the Trojan Wave Packets (assuming only essential
2 dimensions) may be obtained from the total Coulomb + the centrifugal potential
V(r)= -1/r - m^2 / 2 r^2 which has the minimum at the 1/r^2 - m^2 / r^3 = 0 or at
the quantized Bohr radius r_m = m^2. While expanding it around this value up to the
second order one gets the second derivative -2 / r^3 + 3 m^2 /r^4 = 1 /m^6 = omega^2 or
the square of the Kepler frequency for m and so phi_c = Exp [-omega/2 (r - r_m)^2] Exp [i m phi] (
all non Cartesian-looking terms of the Lapacian curvature were either neglected or removed by
the 1/r^(1/2) slow envelope assuming the constant later). So when m is growing the distance between
the two r_m s is 2 m while the width of the Gaussians scales like m^(3/2) and so the ratio as
1/m^(1/2) and the neighboring states become almost the same. Therefore the dipole matrix element
of the Stark x = r Cos(phi) = r (Exp [i phi] + Exp [- i phi])/2 between two circular states can be
found as tridiagonal in m x m and equal r_m/2 taking the same radial functions in the integral
and so leading to the pendulum Hamiltonian. While the progressive with the growing m similarity of the eigenstates will also occur for the nodal excitations of those Gaussians and they are also localized mainly around n^2 this value also remains approximate for the manifolds with the small deviation from circularity i.e. with the radial functions being the excited states of the radial oscillator.
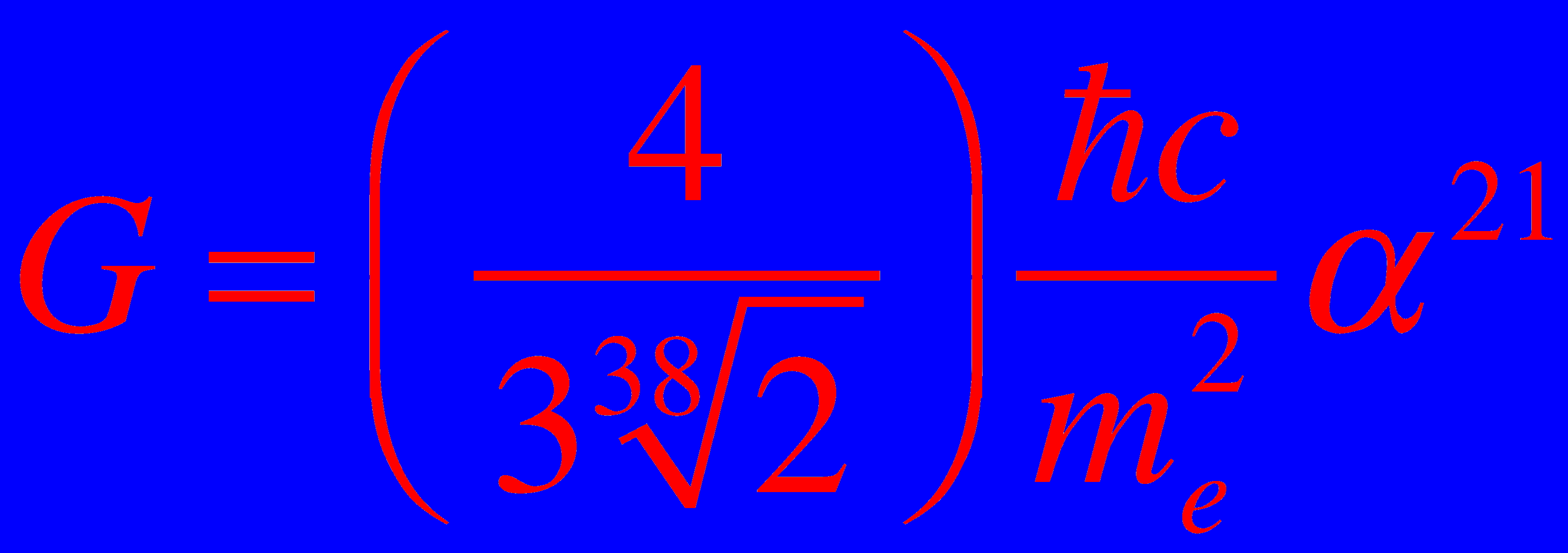
Relation between the Gravitational constant and the Plack constant: The good approximate relation can be found between the Gravitational constant G and the Planck constant in terms of the electron mass, electron charge, speed of light and the vacuum dielectric constant showing that for the electron the electron-electron gravitational interaction is effectively the
electromagnetic electrostatic interaction in the 20-th order power of the fine structure constant alpha = e^2/(4 Pi eplilon0 hbar c) =1/137, G =(4/3)* alpha^20 (e/m_e)^2 /(4 Pi epsilon 0) = 6.79769*10^-11 m^3/(kg s^2).
The simple correcting prefactor 1/2^(1/38) is further perfectly adjusting the value to the best known
CODATA experimental value
G = 1/2^(1/38) (4/3) alpha^21 hbar c / m_e^2 = 6.674330065689801* 10^-11 m^3/(kg s^2) approx (130923/100000) alpha^21 hbar c / m_e^2
or G = alpha^21 G_s where G_s = 4.98 * 10^34 m^3/(kg s^2) is the
strong gravity constant
defined with the electron mass as G_s = (4/3/2^(1/38))*hbar c/ m_e^2 . It may be interpreted as a difference factor between the gravitational self energy radius r_g and the electromagnetic electron radius r_e of the (double)-sperical electron when the gravitational self energy is assumed (4/3) alpha^20 quantum fraction of the the electrostatic one i.e. E_g = G m_e^2/r_g = (4/3) alpha^20 E_e, E_e = m_0 c^2 = (1/4 Pi epsilon0) e^2/r_e i.e r_e = 2^(1/38) r_g.
New "recursion" for constuction of Prime numbers: 3*5*7*11*13*17*19 + 16 = 4849861 is the prime so the product of consecutive primes truncated from below p1*p2*p3*...*pn + p_(n-1) -1 is suspected to be a prime. And that is true:
251*257*263*269*271*277*281*283*293*307 + 292 = 2450545014212368058748731,
29*31*37*41*43*47*53*59*61*67*71*73*79*83*89*97 + 88 = 10334565887047481278774629449
and
13*17*19*23*29*31*37*41*43*47*53*59*61*67*71*73*79*83*89*97*101*103*
107*109*113*127*139 + 126 = 241563763881944601854600574313688430300336818063,
17*19*23*29*31*37*41*43*47*53*59*61*67*71*73*79*83*89*97*101*103*107*
109*113*127*139*149*151*163*167*173*179*181*191*193*197*199*199*211*
223*227*229*233*239*241*251*257*263*269*271*277*281*283*293*307*311*
313*317*331*337*347 + 336 = 1762503776386292745308370810771909419876480566799683391925589283979944
895109766165668620786259739078990334032251067620776133766987
are primes.
The Mersenne number much larger than the largest currently known 51-st Mersenne prime (2^82589933-1) 2^(172279571) - 1 is not a prime !!! Its Fermat divisor is 25*172279571 + 1 = 8613978551 which is a prime. It failes the Mathematica Monte Carlo Fermat little theorem test with one small divisor hyphotesis: Do[a = RandomInteger[1000]; b = PrimeQ[a*2*172279571 + 1];
If[b == True,
Print[b, " ", a,
IntegerQ[(2^(172279571) - 1)/(a*2*172279571 + 1)]]], {i, 1, 10000}] for a = 25. The next Mersenne number 2^(172279589) - 1 is also failing the test and also almost immediately on above 1GHz processor at least on the prime divisor 51*172279589 + 1 = 17572518079. Both numbers having above 170 million binary digits and so above quarter of that decimal estimated check time on
Prime95
project cluster application is above 1 year.
New giant Mersenne numbers excluded:
Mersenne number 2^13730539469-1 is not a prime: ultra-small edge Fermat divisor 19*2*13730539469+1 = 521760499823 (Mathematica)
Mersenne number 2^58501120901-1 is not a prime: ultra-small edge Fermat divisor 13384*2*58501120901+1 = 1565958004277969 (Mathematica,PariGP
)
The quadruple nested Mersenne 2^(2^(2^(2^n-1))-1)-1)-1) =2^(2^127-1)-1), Mn=2^170141183460469231731687303715884105727 - 1 is most likely the prime !!! It is passing the long time small Fermat divisor test. Note that the Lucas-Lehmer test
test performing the large integers multiplication with the Fast Fourier transform calculating the convolution
of two integer numbers as their Fourier transforms product as they were discrete functions with the grid values being the coefficients multiplying the powers of the base of the numerical system scales numerically to the split operator method calculating the complex exponent of the kinetic energy Laplace operator as the e^ik^2 multiplication on the grid size equal twice the value of the exponent. The LL test for then=170141183460469231731687303715884105727 corresponds therefore to the Helium integration on the 6-dimensional hypercube of the edge grid resolution n^(1/6)=2642245 approximately 8*512*512 of points in one dimension and running the n time steps. It would take approximately 10^27 years to conduct the test if only 1ms per iteration (the corresponding Schrödinger equation time step).
Quantum kaleidoscops with BEC in 1D optical lattice with oscillatory interaction
Ergodicity of quantum phase in three state model
Trojan wave packets (or Bohr atom if someone cares less about quantization -
Rutherford-Nagaoka atom) observed in the lab:
Arbitrary multipulse fieldcan generate arbitrary quantum state from other arbitrary state within the Hydrogen all bound states manifold but can one generate high angular momentum Trojan Wavepacket directly with one "pulse" from easy to prepare zero angular momentum static field Stark State ?:
I originally discovered
Trojan wave packets
as follows: The Hamiltonian
in two dimensions in circular coordinates is: H=-hbar^2/2m(d^2/r^2 dphi^2
+ 1/r d/dr + d^2/dr^2) - w (hbar/i)(d/dphi) - 1/r - e r Cos(phi) .
First I assumed that the wave function has a large angular momentum
phase simply Psi -> Psi Exp(i l phi). The new wave function Psi
fulfills the
Schrodinger equation
with the Hamiltonian
H= -hbar^2/2m d^2/dr^2 +hbar^2/2m (l^2/r^2) - 1/r - hbar^2/2 m r^2 d^2/dphi^2
-i l hbar^2/m r^2 d/ dphi - w (hbar/i)(d/dphi) - e r Cos(phi). This Hamiltonian is still nonseparable
so I applied
Hartree
approximation to the coordinate as it was of
1D particle. Simply H = H_r + H_phi, H_r= -hbar^2/2m d^2/dr^2 +hbar^2/2m (l^2/r^2) - 1/r and H_phi = - hbar^2/2 m r_0^2 d^2/dphi^2 - e r_0 Cos(phi) where
selfconsistently Hartree averages were used r_0=Av(r), Av(d/dphi)=0, Av(d/dr)=0
to decouple to separability.
The wave function is therefore a product of an approximate Gaussian in
r localized around r_0 from locally
harmonic normal centrifugal potential + Coulomb potential and the Mathieu
function in phi. Trojan wave packet is here the localized inverted pendulum state and
the anty-Trojan the ground state. This is opposite to the more exact Mathieu theory, the spectrum is inverted
and of the pendulum mass 1 but not -1/3
and the exact classical stability of equilibrium points is opposite but it
predicts both packets right where they are at phi=0 and phi=Pi points having theangular momentum hbar l= m w r_0^2/hbar and approximately right energies.
The natural consequence is the existence of
double-Trojan states in Helium and
the mutual stabilization of two parallel Trojan trajectories in hoop earrings configuration in the magnetic field:
Trojan wave packets of Deuterium nuclei and their fusion products in Palladium,
Helium and Tritium
may be an ultimate solution of
cold fussion theory
as simply normal
hot fussion
when the Deuterium nucleus in Trojan state
supported by the time-dependent fields of passing charges of Palladium lattice makes
a critical collision path slaloming on trajectories that are
Trojan-like in pieces in small critical bulk mass
to cause the fusion-collision-fusion chain reaction in closely packed Deuterium
because
of the dense space localization of curly trajectory (normally of the
order of kiloton in Platinium Deuteride).
Because the primary chain reaction would be
fusion - Rutherford scattering of products 3T1+ and p+ with Deuterium + (activation) - 2 x fusion
and the
Deuterium nuclei are very small to heavy elements the critical
radius of Palladium sphere to start the cascade without slaloming is much above the fission devices and above 10 meters and the critical mass of Deuterium
saturated Palladium is above 10 000 tons.
It is essential to improve the trajectories with cyclotronic slaloming with the alternating ultra-strong magnetic field or otherwise to reduce the bulk.
and |X2>=(|100> - |211>)/2^0.5 and E(2)=E1-d e (anty-Trojan wavepacket), d=128/243 a0. The first eigenstate is of the type 1 + Exp (i phi) while
the other 1 - Exp (i phi) for any fixed r. Therefore the first eigenstate
density is like cos(phi) localized around the angle phi=0 while the second is
Pi-shifted. The radial localization is due to the overlap between two
hydrogen states in r. Very clear banana-like shape of the packet can
be obtained in two-level approximation when one elevates the
excited n=2
component of the state by small detuning from the energy difference
so the relative radial contributions from both states are equal at overlap between a0 and 4a0.
One may therefore notice that the different energies of Trojan and anty-Trojan wave packet is also the
Autler-Townes splitting.
For the larger and larger n (w=E_(n+1)-E_n, l=m=n-1) wavepackets sharply focus relatively to the atom size as the 1/n effect.
